Three types of problems must be considered.
In all cases A and B
are real symmetric (or complex Hermitian) and B is positive definite.
These decompositions are computed for real symmetric matrices
by the driver routines
PxSYGVX (see section 3.2.4).
These decompositions are computed for complex Hermitian matrices
by the driver routines
PxHEGVX (see subsection 3.2.4).
In each of the following three decompositions,
![]() is real and diagonal with diagonal entries
is real and diagonal with diagonal entries
![]() , and
the columns
, and
the columns ![]() of Z are linearly independent vectors.
The
of Z are linearly independent vectors.
The ![]() are called
eigenvalues and the
are called
eigenvalues and the ![]() are
eigenvectors.
are
eigenvectors.
The approximate error bounds
for the computed eigenvalues ![]() are
are
![]()
The approximate error
bounds
for the computed eigenvectors ![]() ,
which bound the acute angles between the computed eigenvectors and true
eigenvectors
,
which bound the acute angles between the computed eigenvectors and true
eigenvectors ![]() , are
, are
![]()
These bounds are computed differently, depending on which of the above three
problems are to be solved. The following code fragments show how.
EPSMCH = PSLAMCH( ICTXT, 'E' )
UNFL = PSLAMCH( ICTXT, 'U' )
* Solve the eigenproblem A - lambda B (ITYPE = 1)
ITYPE = 1
* Compute the norms of A and B
ANORM = PSLANSY( '1', UPLO, N, A, IA, JA, DESCA, WORK )
BNORM = PSLANSY( '1', UPLO, N, B, IB, JB, DESCB, WORK )
* The eigenvalues are returned in W
* The eigenvectors are returned in A
SUBROUTINE PSSYGVX( ITYPE, 'V', 'A', UPLO, N, A, IA, JA,
$ DESCA, B, IB, JB, DESCB, VL, VU, IL, IU,
$ UNFL, M, NZ, W, -1.0, Z, IZ, JZ, DESCZ,
$ WORK, LWORK, IWORK, LIWORK, IFAIL, ICLUSTR,
$ GAP, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'PSSYGVX did not converge, or B not positive definite'
ELSE IF( N.GT.0 ) THEN
* Get reciprocal condition number RCONDB of Cholesky factor of B
CALL PSTRCON( '1', UPLO, 'N', N, B, IB, JB, DESCB, RCONDB,
$ WORK, LWORK, IWORK, LIWORK, INFO )
RCONDB = MAX( RCONDB, EPSMCH )
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
EERRBD( I ) = ( EPSMCH / RCONDB**2 ) * ( ANORM / BNORM +
$ ABS( W( I ) ) )
ZERRBD( I ) = ( EPSMCH / RCONDB**3 ) * ( ( ANORM / BNORM )
$ / RCONDZ( I ) + ( ABS( W( I ) ) /
$ RCONDZ( I ) ) * RCONDB )
10 CONTINUE
END IF
For example, if ![]() ,
,
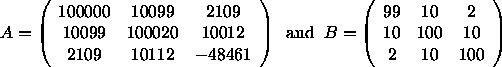
then ![]() ,
,
![]() , and
, and
![]() , and
the approximate eigenvalues, approximate error bounds,
and true errors are
shown below.
, and
the approximate eigenvalues, approximate error bounds,
and true errors are
shown below.
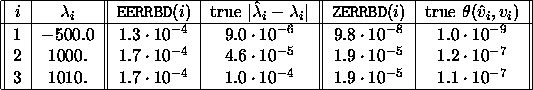
EPSMCH = PSLAMCH( ICTXT, 'E' )
* Solve the eigenproblem A*B - lambda I (ITYPE = 2)
ITYPE = 2
* Compute the norms of A and B
ANORM = PSLANSY( '1', UPLO, N, A, IA, JA, DESCA, WORK )
BNORM = PSLANSY( '1', UPLO, N, B, IB, JB, DESCB, WORK )
* The eigenvalues are returned in W
* The eigenvectors are returned in A
SUBROUTINE PSSYGVX( ITYPE, 'V', 'A', UPLO, N, A, IA, JA,
$ DESCA, B, IB, JB, DESCB, VL, VU, IL, IU,
$ UNFL, M, NZ, W, -1.0, Z, IZ, JZ, DESCZ,
$ WORK, LWORK, IWORK, LIWORK, IFAIL, ICLUSTR,
$ GAP, INFO )
IF( INFO.GT.0 .AND. INFO.LE.N ) THEN
PRINT *,'PSSYGVX did not converge'
ELSE IF( INFO.GT.N ) THEN
PRINT *,'B not positive definite'
ELSE IF( N.GT.0 ) THEN
* Get reciprocal condition number RCONDB of Cholesky factor of B
CALL PSTRCON( '1', UPLO, 'N', N, B, IB, JB, DESCB, RCONDB,
$ WORK, LWORK, IWORK, LIWORK, INFO )
RCONDB = MAX( RCONDB, EPSMCH )
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
EERRBD(I) = ( ANORM * BNORM ) * EPSMCH +
$ ( EPSMCH / RCONDB**2 ) * ABS( W( I ) )
ZERRBD(I) = ( EPSMCH / RCONDB ) * ( ( ANORM * BNORM ) /
$ RCONDZ( I ) + 1.0 / RCONDB )
10 CONTINUE
END IF
For the same A and B as above, the approximate eigenvalues, approximate error bounds, and true errors are shown below.
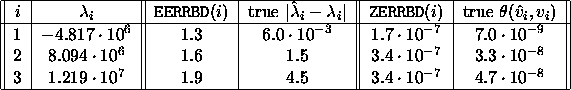
Further Details: Error Bounds for the Generalized Symmetric Definite Eigenproblem
The error analysis of the driver routine PxSYGVX, or PxHEGVX in the complex case
(see section 3.2.4),
goes as follows.
In all cases
![]() is
the absolute gap
between
is
the absolute gap
between ![]() and the nearest other eigenvalue.
and the nearest other eigenvalue.
The angular difference between the computed eigenvector
![]() and a true eigenvector
and a true eigenvector ![]() is
is
![]()
The angular difference between the computed eigenvector
![]() and a true eigenvector
and a true eigenvector ![]() is
is
![]()
The code fragments above replace p(n) by 1 and make sure neither RCONDB nor RCONDZ is so small as to cause overflow when used as divisors in the expressions for error bounds.
These error bounds are large when B is ill-conditioned with respect to
inversion (![]() is large). Often, the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention two ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude:
is large). Often, the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention two ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude:
The second way to get tighter bounds does not actually supply guaranteed
bounds, but its estimates are often better in practice.
It is not guaranteed because it assumes the algorithm is backward stable,
which is not necessarily true when B is ill-conditioned.
It estimates the chordal distance between a
true eigenvalue ![]() and a computed eigenvalue
and a computed eigenvalue ![]() :
:
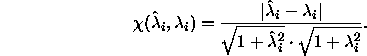
To interpret this measure, we write ![]() and
and ![]() . Then
. Then
![]() .
In other words, if
.
In other words, if ![]() represents the one-dimensional subspace
represents the one-dimensional subspace
![]() consisting of the line through the origin with slope
consisting of the line through the origin with slope ![]() ,
and
,
and ![]() represents the analogous subspace
represents the analogous subspace ![]() , then
, then
![]() is the sine of the acute angle
is the sine of the acute angle ![]() between these
subspaces.
Thus,
between these
subspaces.
Thus, ![]() is bounded by one and is small when both arguments are
large.
is bounded by one and is small when both arguments are
large. It applies only to the first problem,
It applies only to the first problem, ![]() :
:
Suppose a computed eigenvalueof
is the exact eigenvalue of a perturbed problem
. Let
be the unit eigenvector (
) for the exact eigenvalue
. Then if
is small compared with
, and if
is small compared with
, we have
Thusis a condition number for eigenvalue
.