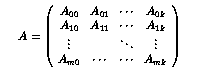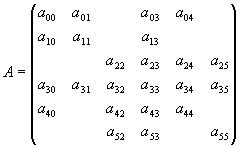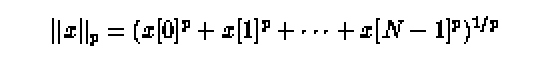Aztec
Руководство пользователя*
Версия 1.1
Скотт А. Хатчинсон(**) Джон Н. Шадид(***) Рей С. Туминаро(****)
Исследовательская лаборатория параллельных исследований
Национальная лаборатория Сандии
Albuquerque, NM 87185
Реферат
Aztec - итерационная библиотека, которая значительно упрощает
процесс распараллеливания при решении систем линейных уравнений Ax =
b, где А - задаваемая пользователем разреженная матрица n
* n, b - задаваемый пользователем вектор длины n и x
- вектор длины n, который должен быть вычислен. Aztec предназначен
для пользователей, не желающих вникать в громоздкие детали параллельного
программирования, но которым необходимо решать системы линейных уравнений
с разреженными матрицами, с эффективным использованием систем параллельной
обработки. Предоставляемые средства трансформации данных позволяют легко
создать распределенные разреженные неструктурированные матрицы для параллельного
решения. После создания распределенной матрицы вычисление может быть выполнено
на любой из параллельных машин, на которых установлен Aztec: nCUBE
2, IBM SP2, Intel Paragon, платформы MPI, а также на обычных последовательных
и векторных платформах.
Для решения систем уравнений Aztec включает ряд итерационных
методов Крылова, таких как метод сопряженных градиентов (CG), обобщенный
метод минимальных невязок (GMRES), метод устойчивого бисопряженного градиента
(BiCGSTAB) и др.. Эти методы Крылова используются совместно с предварительными
преобразованиями, которые повышают обусловленность матриц (полиномиальный
метод и метод декомпозиции областей, использующий LU или неполное LU разложения
в подобластях). Хотя матрица A может быть общего вида, пакет разработан
для матриц, являющихся результатом аппроксимации конечными разностями дифференциальных
уравнений в частных производных (PDEs).
____________
*Данная работа была поддержана программой Applied Mathematical Sciences,
U.S. Department of Energy, Office of Energy Research, и была выполнена
в Sandia National Laboratories для U.S. Department of Energy по контракту
No. DE-AC04-94AL85000. Программный пакет Aztec был разработан авторами
в Sandia National Laboratories и защищен авторскими правами
** Parallel Computational Sciences Department; sahutch@cs.sandia.gov; (505)
845-7996
*** Parallel Computational Sciences Department; jnshadi@cs.sandia.gov;
(505) 845-7876
**** Applied & Numerical Mathematics Department; tuminaro@cs.sandia.gov;
(505) 845-7298
Оглавление
1 Краткий обзор
2 Aztec: общее представление
2.1 Опции Aztec'а
2.2 Параметры Aztec'а
2.3 Статус возврата
3 Форматы данных
3.1
Формат распределенной модифицированной разреженной строки (DMSR)
3.2
Формат распределенной переменной блочной строки (DVBR)
4 Интерфейс данных
высокого уровня
5 Примеры
6 Детальное рассмотрение
тем
6.1 Размещение данных
6.2 Многократная факторизация
6.3 Важные константы
6.4 Подзадачи функции
AZ_transform
7 Функции
Aztec'а
AZ_broadcast
AZ_check_input
AZ_check_msr
AZ_check_vbr
AZ_defaults
AZ_exchange_bdry
AZ_find_index
AZ_find_local_indices
AZ_find_procs_for externs
AZ_free_memory
AZ_gavg_double
AZ_gdot
AZ_gmax_double
AZ_gmax_int
AZ_gmax_matrix_norm
AZ_gmax_vec
AZ_gmin_double
AZ_gmin_int
AZ_gsum_double
AZ_gsum_int
AZ_gsum_vec int
AZ_gvector_norm
AZ_init_quick_find
AZ_invorder_vec
AZ_matvec_mult
AZ_msr2vbr
AZ_order_ele
AZ_print_error
AZ_print_out
AZ_processor_info
AZ_quick_find
AZ_read_msr_matrix
AZ_read_update
AZ_reorder_matrix
AZ_reorder_vec
AZ_set_message_info
AZ_solve
AZ_sort
AZ_transform
Соглашения системы обозначений ________________________________
Для наглядности представления используются различные шрифты, чтобы указать
фрагменты программ, ключевые слова, переменные или параметры. Используемые
соглашения приведены в таблице.
| Шрифт |
Назначение |
| typewriter |
Имена файлов, примеры кода и кодовые фрагменты. |
| sans serif |
Элементы языка C, такие как имена функций и констант, когда они появляются
в тексте или в синтаксисе определения функций. |
| italics |
Имена параметров и переменных, когда они появляются в тексте или в
синтаксисе определения функций |
| AZ_ |
Элементы языка C, такие как имена функций и констант из Aztec
библиотеки. |
Распространение кода библиотеки Aztec _________________________
Aztec открыто доступен для исследовательских целей и может быть
залицензирован для коммерческого применения. Код распространяется через
Internet вместе с технической документацией, примерами C и Fortran программ
и файлами исходных данных. Все это можно получить, контактируя с одним
из авторов, указанных в начале этого документа.
1. Краткий обзор. Aztec - итерационная библиотека, которая значительно
упрощает процесс распараллеливания при решении систем линейных уравнений
Ax = b
где А - задаваемая пользователем разреженная матрица n *
n, b - задаваемый пользователем вектор длины n и x -
вектор длины n, который должен быть вычислен. Aztec предназначен
для пользователей, не желающих вникать в громоздкие детали параллельного
программирования, но которым необходимо решать системы линейных уравнений
с разреженными матрицами, с эффективным использованием систем параллельной
обработки. Самой сложной задачей распараллеливания для пользователя Aztec'а
является спецификация распределенной матрицы для конкретного приложения.
Хотя это может показаться трудным, предоставляемые средства трансформации
данных позволяют создавать распределенные разреженные неструктурированные
матрицы для параллельного решения, с затратами усилий сопоставимыми с затратами
при последовательном программировании. Дополнительную информацию о средствах
трансформации данных можно найти в [5]. После создания распределенной матрицы
вычисление может быть выполнено на любой из параллельных машин, на которых
установлен Aztec: nCUBE 2, IBM SP2, Intel Paragon, платформы MPI,
а также на обычных последовательных и векторных платформах, таких как SUN,
SGI и CRAY.
Aztec включает ряд итерационных методов Крылова, таких как метод
сопряженных градиентов (CG), обобщенный метод минимальных невязок (GMRES),
метод устойчивого бисопряженного градиента (BiCGSTAB) и др. для решения
систем линейных уравнений. Эти методы Крылова используются совместно с
предварительными преобразованиями, которые повышают обусловленность матриц
(полиномиальный метод и метод декомпозиции областей, использующий LU или
неполное LU разложения в подобластях). Дополнительная информация об итеративных
методах и предварительных преобразованиях содержится в [4]. Хотя матрица
A может быть общего вида, пакет разработан для матриц, являющихся
результатом аппроксимации конечными разностями дифференциальных уравнений
в частных производных (PDEs). Подчеркнем, что предварительные преобразования,
итерационные методы и средства распараллеливания ориентированы на системы,
появляющиеся из PDE приложений. Наконец, Aztec может использовать
одно из двух представлений разреженных матриц: поэлементный формат модифицированной
разреженной строки (MSR) или блочный формат переменной блочной строки (VBR).
Параллельная реализация указанных форматов называется "распределенными"
форматами DMSR и DVBR.
Далее в руководстве описывается, как вызывать Aztec из приложения.
Aztec написан на ANSI-стандарте C, поэтому индексы массивов в описании
начинаются с 0. Все прототипы функций представлены в формате ANSI C. В
разделе 2 приводятся итерационные методы, предварительные преобразования
и критерии сходимости. Раздел 3 объясняет, как в Aztec'е поддерживаются
векторы и разреженные матрицы. В разделе 4 обсуждаются средства для создания
распределенных векторов и матриц. Конкретные детализированные примеры,
использующие эти средства, даются в разделе 5, а некоторая дополнительная
информация обсуждается в разделе 6. И наконец, в разделе 7 дается глоссарий
функций Aztec'а, доступных для пользователя.
Оглавление
2. Aztec: общее представление. Для успешного вызова Aztec'а
должны быть выполнены следующие шаги:
- описание параллельной машины (т.е. числа процессоров)
- инициализация матричных и векторных структур данных
- выбор итерационного метода, предварительных преобразований для повышения
обусловленности матриц и критерия сходимости
- инициализация правой части и начальных значений
- вызов подпрограммы решения.
Пример________________________________________________________
#include "az_aztec.h"
void main(void) {
AZ_processor_info(proc_config);
init_matrix_vector_structures(bindx, val, update, external,
update_index, extern_index, data_org);
init_options(options, params);
init_guess_and_rhs(x, b, data_org, update, update_index);
AZ_solve(x, b, options, params, bindx, val, data_org, status,
proc_config);
}
Рис. 1. Программа, использующая Aztec.
На рис. 1 показан образец программы на C, в котором опущены описания
и некоторые параметры. (Примечание. Дистрибутив полной основной
программы содержится в файле az.main.c). Функции init_matrix_vector_structures,
init_options и init_guess_and_rhs создаются пользователем. В
этом разделе мы даем обзор характерных особенностей Aztec'а, описывая
входные массивы пользователя options и params, которые задаются
пользователем в функции init_options. Описание других подпрограмм
приведено в разделах 4 и 5.
2.1. Опции Aztec'а. options - это целочисленный массив
длины AZ_OPTIONS_SIZE, задаваемый пользователем. Он используется
(но не изменяется) функцией AZ_solve для выбора метода решения,
предварительного преобразования для повышения обусловленности матриц и
т.д. Ниже приведены каждая из возможных опций. В некоторых из них есть
ссылки на определяемые пользователем значения options или params,
которые должны быть заданы. Они описагы ниже, но читатель может "перескочить",
почитать о них и вернуться.
Спецификации __________________________________________________
| options[AZ_solver] |
Специфицирует алгоритм решения. По умолчанию: AZ_gmres. |
|
AZ_cg
|
Метод сопряженных градиентов (применяется только к симметричным, положительно
определенным матрицам).
|
|
AZ_gmres
|
|
|
AZ_cgs
|
|
|
AZ_tfqmr
|
|
|
AZ_bicgstab
|
|
|
AZ_lu
|
|
| options[AZ_scaling] |
Специфицирует алгоритм масштабирования. Вся матрица масштабируется
(запись идет на место старой). Кроме того, при необходимости масштабируются
правая часть, начальные данные и полученное решение. По умолчанию: AZ_none. |
|
AZ_none
|
|
|
AZ_Jacobi
|
|
|
AZ_BJacobi
|
Блочное масштабирование Якоби, где размер блоков соответствует VBR блокам.
Точечное масштабирование Якоби применяют, когда используется MSR формат.
|
|
AZ_row_sum
|
Масштабирование каждой строки такое, что сумма ее элементов равна 1.
|
|
AZ_sym_diag
|
Симметричное масштабирование такое, что диагональные элементы равны
1.
|
|
AZ_sym_row_sum
|
|
| options[AZ_precond] |
Специфицирует переобуславливатель. По умолчанию: AZ_none. |
|
AZ_none
|
|
|
AZ_Jacobi
|
Шаг k Якоби (блок Якоби для DVBR матриц, где каждый блок соответствует
VBR блоку). Число шагов k Якоби задается через options[AZ_poly_ord].
|
|
AZ_Neumann
|
Ряд полиномов Неймана, где степень полинома задается через options[AZ_poly_ord].
|
|
AZ_ls
|
Полином наименьших квадратов, где степень полинома задается через options[AZ_poly_ord].
|
|
AZ_lu
|
Повышение обусловленности матриц методом декомпозиции областей (аддитивная
процедура Шварца), использующим разреженную LU факторизацию с допуском
снижения params[AZ_drop] на подматрице каждого процессора.
Обработка внешних переменных в подматрице определяется с помощью options[AZ_overlap].
Разреженная LU факторизация обеспечивается пакетом y12m [6].
|
|
AZ_ilu
|
Подобно AZ_lu, но используется ilu(0) вместо LU.
|
|
AZ_bilu
|
Подобно AZ_lu, но используется ilu(0) вместо LU, где каждый блок
соответствует VBR блоку.
|
|
AZ_sym_GS
|
k-шаговый симметричный метод Гаусса-Зейделя неперекрывающей декомпозиции
области (аддитивная процедура Шварца). В частности, используется симметричная
процедура Гаусса-Зейделя декомпозиции области, где каждый процессор независимо
выполняет один шаг симметричного метода Гаусса-Зейделя на его локальной
матрице, после чего с помощью межпроцессорной коммуникации обновляются
граничные значения перед следующим локальным шагом Гаусса-Зейделя. Число
шагов k задается через options[AZ_poly_ord].
|
| options[AZ_conv] |
Определяет выражение невязки, используемое для подтверждения сходимости
и печати. По умолчанию: AZ_r0. Итерационное решение завершается,
если соответствующее выражение невязки меньше, чем params[AZ_tol]: |
|
AZ_r0
|
|
|
AZ_rhs
|
|
|
AZ_Anorm
|
|
|
AZ_sol
|
|
|
AZ_weighted
|
|
| options[AZ_output] |
Специфицирует информацию, которая должна быть выведена (выражения невязки
см. options[AZ_conv]). По умолчанию: 1. |
|
AZ_all
|
Выводит на печать матрицу и индексирующие векторы для каждого процессора.
Печатает все промежуточные выражения невязок.
|
|
AZ_none
|
|
|
AZ_warnings
|
|
|
AZ_last
|
|
|
>0
|
|
| options[AZ_pre_calc] |
Показывает, использовать ли информацию о факторизации из предыдущего
вызова AZ_solve. По умолчанию: AZ_calc. |
|
AZ_calc
|
|
|
AZ_recalc
|
Использовать информацию предварительной обработки из предыдущего вызова,
но повторно вычислять переобуславливающие множители. Это прежде всего предназначено
для программ факторизации, которые выполняют символьную стадию.
|
|
AZ_reuse
|
Использовать переобуславливатель из предыдущего вызова AZ_solve,
но переобуславливающие множители повторно не вычислять. Кроме того, использовать
масштабирующие множители из предыдущего обращения для масштабирования правой
части, начальных данных и окончательного решения.
|
| options[AZ_max_iter] |
Максимальное число итераций. По умолчанию: 500. |
| options[AZ_poly_ord] |
Степень полинома при использовании полиномиального переобуслапвливателя.
А также число шагов при переобуславливании Якоби или симметричном переобуславливании
Гаусса-Зейделя. По умолчанию: 3. |
| options[AZ_overlap] |
Определяет подматрицы, факторизуемые алгоритмами AZ_lu, AZ_ilu,
AZ_bilu декомпозиции области. По умолчанию: AZ_none. |
|
AZ_none
|
Факторизовать определенную на этом процессоре локальную подматрицу,
отбрасывая столбцы, которые соответствуют внешним элементам.
|
|
AZ_diag
|
Факторизовать определенную на этом процессоре локальную подматрицу,
расширенную диагональной ( блочно-диагональной для VBR формата) матрицей.
Эта диагональная матрица соответствует диагональным элементам строк матрицы
(найденных на других процессорах), связанных с внешними элементами. Это
можно рассматривать как выполнение одного шага Якоби для обновления внешних
элементов и последующего выполнения декомпозиции области с AZ-none
на уравнениях невязки.
|
|
AZ_full
|
Факторизовать определенную на этом процессоре локальную подматрицу,
расширенную строками (найденными на других процессорах), связанными с внешними
переменными (отбрасывая столбцы, связанные с переменными, не определенными
на этом процессоре). Результирующая процедура - аддитивная процедура Шварца
с совмещением.
|
| options[AZ_kspace] |
Размер подпространства Крылова для перезапущенного GMRES. По умолчанию:
30. |
| options[AZ_orthog] |
Схема ортогонализации GMRES. По умолчанию: AZ_classic. |
|
AZ_classic
|
|
|
AZ_modified
|
|
| options[AZ_aux_vec] |
Определяет  (вектор, необходимый
в некоторых итерационных методах). Поведение сходимости в зависимости от
его установки изменяется незначительно. По умолчанию: AZ_resid. (вектор, необходимый
в некоторых итерационных методах). Поведение сходимости в зависимости от
его установки изменяется незначительно. По умолчанию: AZ_resid. |
|
AZ_resid
|
|
|
AZ_rand
|
 устанавливается в набор случайных
чисел между -1 и 1. ЗАМЕЧАНИЕ: При использовании этой опции сходимость
зависит от числа процессоров (т.е. итерации, полученные на x процессорах,
отличаются от итераций, полученных на у процессорах, если x
не равно y). устанавливается в набор случайных
чисел между -1 и 1. ЗАМЕЧАНИЕ: При использовании этой опции сходимость
зависит от числа процессоров (т.е. итерации, полученные на x процессорах,
отличаются от итераций, полученных на у процессорах, если x
не равно y).
|
2.2. Параметры Aztec'а. params - это массив двойной точности
пользователя, обычно длины AZ_PARAMS_SIZE. Однако, когда для проверки
сходимости необходим вектор веса (т.е. options[AZ_conv]
= AZ_weighted), он добавляется в params, чья длина теперь
должна быть AZ_PARAMS_SIZE + число элементов, модифицируемых на
этом процессоре. В любом случае содержимое params используется (но
не изменяется) функцией AZ_solve, чтобы управлять поведением итерационных
методов. Элементы массива определены следующим образом:
Спецификации __________________________________________________
| params[AZ_tol] |
Определяет значение допуска, используемое вместе с тестами сходимости.
По умолчанию: 10-- 6 |
| params[AZ_drop] |
Определяет допуск снижения, используемый вместе с LU переобуславливателем.
По умолчанию: 0.0. |
| params[AZ_weights] |
Когда options[AZ_conv] = AZ_WEIGHTED, i-ая
локальная компонента вектора веса хранится в элементе params[AZ_weights+i]. |
Рис. 2 показывает пример функции init_options, где Aztec
функция AZ_DEFAULTS устанавливает опции по умолчанию.
Пример ________________________________________________________
void init_options(int options [AZ_OPTIONS_SIZE],
double params[AZ_PARAMS_SIZE])
{
AZ_defaults(options, params);
options[AZ_solver] = AZ_cgs;
options[AZ_scaling] = AZ_none;
options[AZ_precond] = AZ_ls;
options[AZ_output] = 1;
options[AZ_max_iter] = 640;
options[AZ_poly_ord] = 7;
params[AZ_tol] = 0.0000001;
}
Рис. 2. Пример программы init_options инициализации опций.
2.3. Статус возврата. status - массив двойной точности
длины AZ_STATUS_SIZE, возвращаемый из AZ_solve. (Примечание.
Вся целочисленная информация, возвращенная из AZ_solve, переведена
в вещественные значения двойной точности и хранится в status.) Содержание
status описано ниже.
Спецификации __________________________________________________
| status[AZ_its] |
Число итераций, выполненных итерационным методом. |
| status[AZ_why] |
Причина завершения программы AZ_solve. |
|
AZ_normal
|
Критерий сходимости, который запросил пользователь, удовлетворен.
|
|
AZ_param
|
|
|
AZ_breakdown
|
|
|
AZ_loss
|
|
| AZ_ill_cond |
Метод Хейссенберга в GMRES некорректен. Это может быть вызвано сингулярной
матрицей приложения. В этом случае GMRES пробует вычислять решение наименьшими
квадратами.
|
|
AZ_maxits
|
Максимум итераций, выполненных без сходимости.
|
| status[AZ_r] |
Истинная норма невязки, соответствующая выбору options[AZ_conv]
(эта норма вычисляется, используя полученное решение). |
| status[AZ_scaled_r] |
Истинное выражение отношения невязки как определено в options[AZ_conv]. |
| status[AZ_rec_r] |
Норма, соответствующая options[AZ_conv] конечной
невязки или оцененной конечной невязки (рекурсивно вычисленной итерационным
методом). Замечание: При использовании 2-нормы tfqmr вычисляет оценку
остаточной нормы вместо вычисления невязки. |
После ненормального выхода из AZ_solve пользователь может предпочесть
перезапуск, используя текущее вычисленное решение в качестве начального
приближения.
Оглавление
3. Форматы данных. В этом разделе описываются внутренние матричные
и векторные форматы Aztec'а. В разделе 4 мы обсуждаем средство,
преобразующее данные из более простого формата в этот формат. Далее термины
"элемент" и "компонента" используются взаимозаменяемо,
обозначая определенную составляющую вектора, к которой можно получить доступ.
Базисной операцией Aztec'а является произведение разреженной
матрицы на вектор y <- Ax. Чтобы выполнить эту операцию параллельно,
векторы x, у и матрица A должны быть распределены по процессорам.
Элементы любого вектора длины n назначаются определенному процессору
с помощью некоторого метода разбиения (например, Chaco [2]). При
вычислении элементов в векторе y процессор вычисляет только те элементы
в у, которые ему были назначены. Эти векторные элементы непосредственно
хранятся в процессоре и определяются индексами из множества update
(изменяемые) для данного процессора. Множество update разделено
на два подмножества: internal (внутренние) и border (граничные).
Компонента, соответствующая индексу из множества internal, модифицируется
с использованием информации только текущего процессора. Например, индекс
i является internal, если в базисном матрично-векторном произведении
элемент yi модифицируется этим процессором и если каждый
j, определяющий ненулевой Aij в строке i,
содержится в update. Множество border определяет элементы,
которые потребовали бы значения от других процессоров для обновления при
матрично-векторном произведении. Например, индекс i принадлежит
border, если в базисном матрично-векторном произведении элемент
yi модифицируется этим процессором и если существует
по крайней мере один j, связанный с ненулевым Aij
из строки i, который не содержится в update. В матрично-векторном
произведении множество индексов называется external (внешние), если
они указывают на не принадлежащие процессору элементы в x, которые
необходимы для вычисления компонентов, соответствующих border индексам,
Внешние компоненты сохраняются в других процессорах и передаются из них
через межпроцессорную связь всякий раз при выполнении матрично-векторного
произведения. Рисунок 3 поясняет, как определить упомянутые множества при
распределении вершин сетки .

Рис. 3. Пример распределения конечно-разностной сетки.
Так как эти множества индексов используются только для доступа к специфическим
векторным компонентам, такие же имена (то есть update, internal, border,
external) иногда используются ниже, чтобы описать собственно векторные
элементы. Обобщая эти обозначения, различают три типа векторных элементов,
локально сохраняя сначала internal компоненты, затем border
компоненты и, наконец, external компоненты. Кроме того, все external
компоненты, полученные от одного процессора, сохраняются последовательно.
Ниже мы суммируем терминологию для процессора с общим числом элементов
N, где N_internal, N_border и N_ external элементов
распределяются соответственно по множествам internal, border и external.
| множество |
описание |
локальная нумерация |
|
internal
|
модифицируется без коммуникации |
от 0 до N_internal - 1 |
|
border
|
модифицируется с коммуникацией |
от N_internal до N_internal+ N_border-1. |
|
external
|
не модифицируется, но используется для модификации border |
от N_internal + N_border до N -1.
элементы, полученные от одного процессора, нумеруются последовательно. |
Подобно векторам, подмножество матричных ненулевых элементов хранится
в каждом процессоре. В частности, каждый процессор хранит только те строки,
которые соответствуют его множеству update. Например, если векторный
элемент i модифицируется на процессоре p, то процессор p
также хранит все ненулевые элементы i-ой строки матрицы. Далее,
локальная нумерация векторных элементов на определенном процессоре индуцирует
локальную нумерацию матричных строк и столбцов. Например, если векторный
элемент k локально пронумерован как kl, то все
ссылки на строку k или столбец k в матрице были бы локально
пронумерованы как kl. Таким образом, каждый процессор
содержит подматрицу, чьи элементы по строкам и столбцам соответствуют переменным,
определенным на этом процессоре.
Остальная часть этого раздела описывает два разреженных матричных формата,
которые используются для хранения локальной перенумерованной подматрицы.
Эти два разреженных матричных формата соответствуют общим форматам, используемым
в последовательных вычислениях.
3.1. Формат распределенной модифицированной разреженной строки (DMSR).
Формат DMSR - обобщение формата MSR [3]. Структура данных состоит из целочисленного
вектора bindx и вектора двойной точности val, каждый длины
N_nonzeros + 1, где N_nonzeros есть число ненулевых элементов
в локальной подматрице. Для подматрицы с m строками массивы DMSR
имеют следующий вид:
| bindx: |
| |
bindx(0) |
= m + 1 |
| |
bindx[k+1]-bindx[k] |
= число отличных от нуля недиагональных элементов в k-ой строке,
где k < m |
| |
bindx[ks,...ke] |
= индексы столбца отличных от нуля недиагональных элементов в k-ой
строке, где
ks = bindx[k] и ke = bindx[k+1]-1. |
| val: |
| |
val[k] |
= Akk, k< m |
| |
val[ki] |
= (k,bindx[ki])-ому матричному элементу, где  и ks , ke определены выше.
и ks , ke определены выше. |
Замечание: val[m] не используется. См. [1] для детального обсуждения
формата MSR.
3.2. Формат распределенной переменной блочной строки (DVBR).
Формат распределенной переменной блочной строки (DVBR) является обобщением
формата VBR [1]. Структура данных состоит из вектора двойной точности val
и пяти векторов целого типа: indx, bindx, rpntr, cpntr и bpntr.
Этот формат лучше всего подходит для разреженных блочных матриц вида
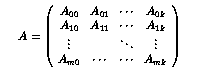
где Aij обозначает блок (или подматрицу). В разреженной
блочной матрице некоторые из этих блоков могут быть полностью нулевыми,
в то время как другие могут быть плотными. Ниже описаны DVBR векторы для
матрицы с M * K блоками.
rpntr[0 ... M]:
| |
rpntr[0] |
= 0 |
| |
rpntr[k+1] - rpntr[k] |
= число строк в k-ой блочной строке |
cpntr[0 ... K]:
| |
cpntr[0] |
= 0 |
| |
cpntr[k+1] - cpntr[k] |
= число столбцов в k-ом блочном столбце |
bpntr[0 ... M]:
| |
bpntr[0] |
= 0 |
| |
bpntr[k+1] - bpntr[k] |
= число ненулевых блоков в k-ой блочной строке |
bindx[0 ... bpntr[M] ]:
| |
bindx[ks ... ke] |
= индексы блочных столбцов ненулевых блоков в блочной строке k,
где ks = bpntr[k] и ke = bpntr[k+1]-1 |
indx[0 ... bpntr[M] ]:
| |
indx[0] |
= 0 |
| |
indx[ki+1] - indx[ki] |
= число ненулевых элементов в (k, bindx[ki])-ом блоке,
где  с ks
и ke, определенными выше. с ks
и ke, определенными выше. |
val[0 ... indx[bpntr[M]] ]:
| |
val[is ... ie] |
= ненулевые элементы в (k, bindx[ki])-ом блоке, хранимым
в столбце главного порядка, где ki определен выше, is
= indx[ki] и ie = indx[ki+1]-1 |
Формат VBR детально обсуждается в [1].
Оглавление
4. Интерфейс данных высокого уровня. Установка распределенного
формата, описанного в разделе 3 для локальной подматрицы на каждом процессоре
может быть очень громоздкой. В частности, пользователь должен определить
соответствие между глобальной и локальной нумерациями, что облегчает правильную
коммуникацию. Кроме того, должны быть установлены дополнительные переменные
для коммуникации и синхронизации (см. раздел 6).
В этом разделе мы описываем более простой формат данных, который используется
вместе с функцией преобразования для генерирования структур данных для
Aztec'а. Новый формат позволяет пользователю определять строки в
естественном порядке, а также использовать глобальные номера столбцов в
массиве bindx. Чтобы использовать функцию преобразования, пользователь
готовит множество update и подматрицу для каждого процессора. Однако,
в отличие от предыдущего раздела, подматрица определяется, используя глобальную
нумерацию координат вместо локальной нумерации, требуемой Aztec'ом.
Эта процедура значительно облегчает матричную спецификацию, являясь главным
преимуществом системы преобразования.
На данном процессоре множество update (т.е. назначенные процессору
векторные элементы) определяется инициализацией массива update на
каждом процессоре так, чтобы оно содержало глобальный индекс каждого элемента,
назначенного процессору. Массив update должен сортироваться в порядке
возрастания (т.е. i < j => update[i] < update[j]). Эта
сортировка может выполняться с помощью Aztec функции AZ_sort.
Спецификация матриц выполняется с использованием массивов, определенных
в предыдущем разделе. Однако, теперь локальные строки определяются в том
же порядке, как и массив update, а индексы столбцов (например, bindx)
указываются как глобальные индексы столбцов. Чтобы пояснить это более подробно,
рассмотрим следующую матрицу:
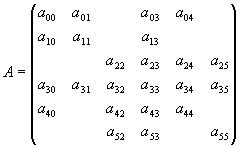
Рисунок 4 поясняет информацию, соответствующую
определенному разбиению матрицы, которое задается пользователем как входная
информация для программы преобразования данных. Используя эту информацию,
AZ_transform:
- определяет множества internal, border и external.
- определяет локальную нумерацию: update_index[i] - это локальная
нумерация для update[i], в то время как extern_index[i] -
локальная нумерация для external[i].
- переставляет и перенумеровывает локальные строки и столбцы подматриц
так, чтобы они соответствовали новому порядку.
- вычисляет дополнительную информацию (например, количество внутренних,
граничных и внешних компонентов на этом процессоре) и сохраняет ее в data_org
(см. раздел 6).
Пример преобразования дается на рисунке 5. и находится
в файле az_app_uitils.c. Утилита Aztec'а AZ_read_update
читает файл и приписывает элементы к update. Пользователь с помощью
программы create_matrix создает MSR или VBR матрицу, используя глобальную
нумерацию. Однажды преобразованная матрица может теперь использоваться
в Aztec'е.
Оглавление
5. Примеры. Завершается описание примера программы (рисунки 1,
2 и 5), фрагменты которой приведены ранее. На рисунке
1 AZ_processor_info - это утилита Aztec'а, которая инициализирует
массив proc_config, сообщая число используемых процессоров и номер
данного процессора. Функция AZ_solve решает подготовленную пользователем
линейную систему. Таким образом, пока не обсуждались функции init_guess_and_rhs
на рисунке 1 и create_matrix на рисунке
5.
Функция init_guess_and_rhs инициализирует начальное приближение
и правую часть уравнения. На рисунке 6 дается пример
программы, которая устанавливает вектор начальных данных в ноль, а вектор
правой части равным глобальным индексам (где локальный элемент update_index[i]
соответствует глобальному элементу update[i], см. раздел 4). (Примечание.
Наоборот, i может заменить update_index[i], вызывая AZ_reorder_vec()
после инициализации rhs.)
Функция create_matrix, инициализирующая MSR матрицу, показана
на рисунке 7. Специальная функция add_row,
реализующая 5-точечный двумерный оператор Пуассона на сетке n * n,
показана на рисунке 8 (n - глобальная переменная,
задаваемая пользователем). Она вычисляет MSR элементы, соответствующие
новой строке матрицы. Заменяя функцию add_row, можно решать различные
матричные задачи. С помощью нескольких строк программы и функций, описанных
ранее, пользователь инициализирует и решает двумерную задачу Пуассона.
Для простоты представления этот пример структурирован, библиотека же Aztec
не предполагает никакой структуры в разреженной матрице. Вся коммуникация
и перенумерация переменных выполняются автоматически без предположения
о структурированной коммуникации.
Вместе с Aztec'ом поставляются (в файле az_examples.c)
другие функции add_row, соответствующие трехмерному уравнению Пуассона
и двумерному уравнению Пуассона старшего порядка. Потенциальным пользователям
эти примеры полезно пересмотреть. Во многих случаях новые приложения можно
написать с помощью простого редактирования этих программ. Заинтересованный
читатель должен заметить, что только несколько строк отличаются в функциях
для 5-точечного оператора Пуассона, уравнения Пуассона старшего порядка
и трехмерного уравнения Пуассона. Кроме того, программы add_row
по существу идентичны тем, которые использовались бы для разреженных матриц
в последовательных приложениях, наконец, они не содержат никаких ссылок
на процессоры, коммуникацию или другую специфику параллельного программирования.
Примеры _______________________________________________________
| proc0: |
| |
N_update: |
3 |
| |
update: |
0 |
1 |
3 |
| |
bindx: |
4 |
7 |
9 |
14 |
1 |
3 |
4 |
0 |
3 |
0 |
1 |
2 |
4 |
5 |
| |
val: |
a00 |
a11 |
a33 |
- |
a01 |
a03 |
a04 |
a10 |
a13 |
a30 |
a31 |
a32 |
a34 |
a35 |
| proc1: |
| |
N_update: |
1 |
| |
update: |
4 |
| |
bindx: |
2 |
5 |
0 |
2 |
3 |
| |
val: |
a44 |
- |
a40 |
a42 |
a43 |
| proc2: |
| |
N_update: |
2 |
| |
update: |
2 |
5 |
| |
bindx: |
3 |
6 |
8 |
3 |
4 |
5 |
2 |
3 |
| |
val: |
a22 |
a55 |
- |
a23 |
a24 |
a25 |
a52 |
a53 |
Рис. 4. Ввод пользователя (MSR формат) для инициализации матричной
задачи из примера.
Пример ________________________________________________________
init_matrix_vector_structures(bindx, val, update, external,
update_index, extern_index, data_org);
{
AZ_read_update(update, N_update);
create_matrix(bindx, val, update, N.update);
AZ_transform(bindx, val, update, external, update_index,
extern_index, data_org, N_update);
}
Рис. 5. init_matrix_vector_structures.
Пример ________________________________________________________
void init_guess_and_rhs(x, rhs, data_org, update, update_index)
{
N_update = data_org[AZ_N_internal] + data_org[AZ_N_border];
for (i = 0; i < N_update ; i = i + 1) {
rhs[update_index[i]] = (double) update[i];
x[i] = 0.0;
}
}
Рис. 6. init_guess_and_rhs.
Пример ________________________________________________________
void create_matrix(bindx, val, update, N_update)
{
N_nonzeros = N_update + 1;
bindx[0] = N_nonzeros;
for (i = 0; i < N_update; i = i + 1)
add_row(update[i], i, val, bindx);
}
Рис. 7. create_matrix.
Пример ________________________________________________________
void add_row(row, location, val, bindx)
{
k = bindx[location]; val[location] = 4.; /* диагональ матрицы */
/* проверка соседних точек по каждому измерению и добавление */
/* ненулевых элементов, если сосед существует. */
bindx[k] = row + 1; if (row%n != n-1) val[k++] = -1.;
bindx[k] = row - 1; if (row%n != 0) val[k++] = -1.;
bindx[k] = row + n; if ((row/n)%n != n-1) val[k++] = -1.;
bindx[k] = row - n; if ((row/n)%n != 0) val[k++] = -1.;
bindx[location+1] = k;
}
Рис. 8. add_row для двумерной задачи Пуассона
Усложнение структур данных приводит к необходимости решения дополнительных
проблем при параллельном программировании с помощью Aztec'а. Чтобы
пояснить это, рассматривается двумерный конечно-разностный пример с треугольной
сеткой сложной геометрии. В отличие от предыдущего примера create_matrix
определяет разреженный шаблон (т.е. bindx), а не фактические ненулевые
элементы (т.е. val), поскольку для их вычисления требуется межпроцессорная
коммуникация. Таким образом, в этом примере AZ_TRANSFORM получает
разреженный шаблон и инициализирует структуры связи данных. Используя эти
структуры, коммуникация может быть выполнена на более поздней стадии при
вычислении ненулевых элементов матрицы.
Рисунок 9 описывает функцию create_matrix,
а на рисунке 10 описана дополнительная функция matrix_fill,
вызов которой следует включить перед вызовом AZ_solve на рисунке
1. Мы не приложили каких-либо усилий для оптимизирования этих программ.
На обоих рисунках подчеркнуты новые строки, добавленные для параллельной
реализации. То есть create_matrix и matrix_fill были созданы
из последовательной конечно-разностной программы разделением ее на две
функции и добавлением нескольких новых строк, необходимых для параллельной
реализации. Единственное дополнительное изменение - это замена единого
файла данных, содержащего чтение с помощью read_triangles данных
о связности треугольников, на набор файлов данных, содержащих связность
треугольников для каждого процессора. Мы не обсуждаем детали этой программы,
а только хотим обратить внимание читателей на малое число строк, которые
надо изменить для преобразования последовательной неструктурированной программы
в параллельную. Большинство основных подпрограмм остаются теми же самыми,
например, setup_Ke, которая вычисляет элементы, и add_to_element,
которая сохраняет элементы в MSR структурах данных. Фактически почти все
новые строки программы соответствуют добавлению коммуникации (AZ_EXCHANGE_BDRY)
(которая была главной причиной отсрочки вычисления ненулевых элементов
матрицы), а также преобразованию глобальных значений индексов в локальные
значения индексов с помощью AZ_FIND_INDEX. В примере задачи Пуассона
все детали, касающиеся коммуникации, скрыты от пользователя.
Пример ________________________________________________________
void create_matrix(bindx, val, update, N_update)
{
read_triangles(T, N_triangles);
init_msr(val, bindx, N_update);
for (triangle = 0; triangle < N_triangles; triangle = triangle + 1)
for (i = 0; i < 3; i = i + 1) {
row = AZ_find_index(T[triangle][i], update, N_update);
for (j = 0; j <3; j = j + 1) {
if (row != NOT_FOUND)
add_to_element(row, T[triangle][j], 0.0, val, bindx, i==j);
} }
compress_matrix(val, bindx, N_update);
}
Рис. 9. create_matrix для конечно-разностной задачи Пуассона
Пример ________________________________________________________
void matrix_fill(bindx, val, N_update, update, update_index,
N_external, external, extern_index)
{
/* Чтение координат x и y из входного файла */
for (i = 0; i < N_update; i = i + 1) {
read_from_file(x[update_index[i]], y[update_index[i]]);
}
AZ_exchange_bdry(x);
AZ_exchange_bdry(y);
/* Локальное перенумерование строк и столбцов */
/* новой разреженной матрицы */
for (triangle = 0; triangle < N_triangles; triangle = triangle + 1){
for (i = 0; i < 3; i = i + 1) {
row = AZ_find_index(T[triangle][i], update, N_update);
if (row == NOT_FOUND) {
row = AZ_find_index(T[triangle][i], external, N_external);
T[triangle][i] = extern_index[row];
}
else T[triangle][i] = update_index[row];
}
}
/* Заполнение элементов плотной матрицы Ke */
for (triangle = 0; triangle < N_triangles; triangle = triangle + 1){
setup_Ke(Ke, x[T[triangle][0]], y[T[triangle][0]],
x[T[triangle][1]], y[T[triangle][1]],
x[T[triangle][2]], y[T[triangle][2]]);
/* Заполнение разреженной матрицы разбрасыванием элементов Ke */
/* в соответствующие места */
for (i = 0; i < 3; i = i + 1) {
for (j = 0; j < 3; j = j + 1) {
if (T[triangle][i] < N_update){
add_to_element(T[triangle][i], T[triangle][j], Ke[i][j],
val, bindx, i==j);
}
}
}
}
Рис. 10. matrix_fill для конечно-разностной задачи Пуассона.
Оглавление
6. Детальное рассмотрение тем.
6.1. Размещение данных. Функция Aztec'а AZ_transform
инициализирует целочисленный массив data_org. Этот массив определяет,
как матрица установлена на параллельной машине. Чаще всего пользователь
не имеет дела с содержимым этого массива. Однако, в некоторых ситуациях
полезно инициализировать его элементы без использования AZ_transform,
обращаться к этим элементам (например, для определения числа internal
компонент) или изменять эти элементы (например, при многократном использовании
информации разложения на множители, см. раздел 6.2). Пользуясь программой
преобразования, пользователь может не интересоваться размерами data_org,
поскольку массив организуется в AZ_TRANSFORM. Однако, когда программа
преобразования не используется, data_org должен быть образован размером
AZ_COMM_SIZE + число векторных элементов, разосланных по другим
процессорам при матрично-векторном умножении. Массив data_org содержит
следующее:
Спецификации __________________________________________________
| data_org[AZ_matrix_type] |
Определяет матричный формат. |
|
AZ_VBR_MATRIX
|
|
|
AZ_MSR_MATRIX
|
|
| data_org[AZ_N_internal] |
Число элементов, модифицируемых данным процессором, которые могут быть
вычислены без информации из соседних процессоров (N_internal). Это
также соответствует числу внутренних строк, назначенных данному процессору. |
| data_org[AZ_N_border] |
Число элементов, модифицируемых данным процессором с использованием
информации от соседних процессоров (N_border). |
| data_org[AZ_N_external] |
Число external элементов, необходимых этому процессору (N_external). |
| data_org[AZ_N_int_blk] |
Число внутренних VBR блочных строк, принадлежащих данному процессору.
Устанавливается в data_org[AZ_N_internal] для MSR
матриц. |
| data_org[AZ_N_bord_blk] |
Число граничних VBR блочных строк, принадлежащих данному процессору.
Устанавливается в data_org[AZ_N_border] для MSR матриц.
|
| data_org[AZ_N_ext_blk] |
Число внешних VBR блочных строк на данном процессоре. Устанавливается
в data_org[AZ_N_external] для MSR матриц. |
| data_org[AZ_N_neigh] |
Число процессоров, с которыми мы обмениваемся информацией (посылаем
или получаем) при выполнении матрично-векторных произведений. |
| data_org[AZ_total_send] |
Общее число векторных элементов, посланных другим процессорам при выполнении
матрично-векторных произведений. |
| data_org[AZ_name] |
Имя матрицы. Это имя используется при выборе предварительного разложения
на множители для повышения обусловленности матрицы (см. раздел 6.2). (Положительное
целое число). |
| data_org[AZ_neighbors] |
Начало вектора, содержащего узловые идентификаторы соседних процессоров.
То есть data_org[AZ_neighbors+i] дает узловой идентификатор
(i+1)-го соседа. |
| data_org[AZ_rec_length] |
Начало вектора, содержащего число элементов, получаемых от каждого
соседа. Мы получаем от (i+1)-го соседа data_org[AZ_rec_length+i]
элементов. |
| data_org[AZ_send_length] |
Начало вектора, содержащего число элементов, посылаемых каждому соседу.
Мы посылаем (i+l)-ому соседу data_org[AZ_rec_length+i]
элементов. |
| data_org[AZ_send_list] |
Начало вектора, указывающего элементы, которые мы пошлем другим процессорам
в процессе коммуникации. Первые data_org[AZ_send_length]
компонент соответствуют элементам первого соседа, следующие data_org[AZ_send_length+1]
компонент - элементам второго соседа, и т.д. |
6.2. Многократная факторизация. При решении задачи Aztec
может создавать некоторую информацию, которая далее может многократно использоваться.
Чаще всего это либо множители, масштабирующие матрицу, либо информация
о переобуславливающей факторизации для LU или ILU. Эта информация сохраняется
системой, доступ к ней осуществляется по имени матрицы, данному data_org[AZ_name].
Изменяя options[AZ_pre_calc] и data_org[AZ_name],
можно реализовать различные возможности Aztec'а. Например, рассмотрим
следующую ситуацию. Пользователь должен решить линейные системы в порядке,
показанном ниже:

Первая и вторая системы решаются с установкой значения AZ_calc
в options[AZ_pre_calc]. Однако, имя (т. е. data_org[AZ_name])
меняется между этими двумя решениями. В этом случае масштабирующая и переобуславливающая
информация, вычисленная в первом решении, не затирается информацией второго
решения. Поэтому, установив в options[AZ_pre_calc]
значение AZ_reuse и установив в data_org[AZ_name]
имя, которое использовалось при первом решении, можно решить третью систему
с повторным использованием информации первого решения о масштабировании
(для масштабирования правой части, начальных предположений и перемасштабирования
окончательного решения) и о переобуславливающей факторизации (например,
ILU). (Примечание. Матрицу нельзя повторно масштабировать, т.к.
масштабированная матрица записывается на место исходной матрицы.) В этом
примере нет необходимости эту же самую матричную систему решать для первого
и третьего случая. В частности, переобуславливатели могут быть повторно
использованы из предыдущих нелинейных итераций, даже при том, что линейная
система после ее решения изменяется. Конечно, информация из предыдущих
решений линейных систем используется не многократно. Поэтому пользователь
должен явно освободить пространство, связанное с матрицей, иначе эта информация
будет оставаться до конца работы программы. Пространство очищается вызовом
AZ_free_memory(data_org[AZ_name]).
6.3. Важные константы. Aztec использует ряд констант, которые
определены в файле az_aztec_defs.h. Большинство пользователей может
игнорировать эти константы. Однако, в некоторых ситуациях константы должны
быть изменены. Ниже - список этих констант с кратким описанием:
| AZ_MAX_NEIGHBORS |
Максимальное число процессоров, с которыми идет обмен информацией при
матрично-векторном произведении. |
| AZ_MSG_TYPE AZ_NUM_MSGS |
Все типы сообщений, используемых Aztec'ом, находятся между AZ_MSG_TYPE
и AZ_MSG_TYPE + AZ_NUM_MSGS - 1. |
| AZ_MAX_BUFFER_SIZE |
Максимальная длина сообщения, которое может быть послано любым процессором
в любое время перед получением. Используется для разделения больших сообщений
во избежание переполнения буфера. |
| AZ_MAX_MEMORY_SIZE |
Максимально доступная память. Используется прежде всего для LU-факторизаций,
где сначала выделяется большой объем памяти, а затем неиспользованные части
после факторизации освобождаются. |
| AZ_TEST_ELE |
Внутренний параметр алгоритма, который может влиять на скорость вычисления
AZ_find_procs_for_externs. Уменьшите AZ_TEST_ELE, если буфера
связи переполняются при этом вычислении. |
6.4. Подзадачи функции AZ_transform. Функция AZ_transform,
описанная в разделе 4, фактически состоит из 5 подзадач. В большинстве
случаев пользователю нет необходимости иметь дело с отдельнымм подзадачами.
Однако, при наличии дополнительной информации некоторые из подзадач могут
быть опущены. Тогда пользователь может отредактировать текст программы
AZ_TRANSFORM в файле az_tools.с для конкретного применения. В этом разделе
мы кратко описываем пять подпрограмм, из которых состоит функция преобразования.
Более детальные описания даются в [5]. Прототипы для этих подпрограмм,
также как для AZ_trasnform, даются в разделе 7.
AZ_transform начинается с идентификации множества external,
которое необходимо каждому процессору. Здесь каждый столбец должен соответствовать
либо элементу, модифицируемому этим процессором, либо external элементу.
Функция AZ_find_local_indices проверяет каждый столбец. Если столбец
находится в update, то его номер заменяется соответствующим индексом
в update (т.е. update[новый индекс столбца] = старый индекс столбца). Если
номер столбца не находится в update, то он хранится в external списке,
и номер столбца заменяется индексом в external (т.е. external[новый индекс
столбца - N_update] = старый индекс столбца).
AZ_find_procs_for_externs запрашивает другие процессоры для определения
тех из них, которые модифицируют каждую из его external компонент. Массив
extern_proc заполняется так, что extern_proc[i] указывает, какой процессор
модифицирует external[i].
AZ_order_ele переупорядочивает external компоненты так, что элементы,
модифицируемые одним и тем же процессором, становятся смежными. Это новое
упорядочивание задается в extern_index, где extern_index[i] указывает локальную
нумерацию для external[i]. Кроме того, update компоненты переупорядочиваются
так, что internal компоненты предшествуют border компонентам. Это новое
упорядочивание задается в border_index, где border_index[i] указывает локальную
нумерацию для update[i].
AZ_set_message_info инициализирует data_org (см. раздел 6.1)
Это реализуется вычислением числа соседей, созданием списка соседей, вычислением
числа значений, которые посылаются каждому соседу и получаются от каждого
соседа, и вычислением списка элементов, которые будут посланы другим процессорам
при коммуникации.
И наконец, AZ_reorder_matrix переставляет и переупорядочивает
ненулевые элементы матрицы так, чтобы их расположение соответствовало только
что переупорядоченным векторным элементам.
Оглавление
7. Функции Aztec'а. В этом разделе мы описываем функции Aztec'а,
доступные пользователю. Вначале описываются некоторые переменные, входящие
в списки параметров многих функций, затем описываются отдельные функции.
Часто используемые параметры Aztec'а __________________________
| data_org |
Массив, описывающий матричный формат (раздел 6.1). Образование массива
и установку его значений выполняют функции AZ_set_message_info и
AZ_transform. |
| extern_index |
extern_index[i] дает локальную нумерацию глобального элемента
external[i]. Образование массива и установку его значений выполняют
функции AZ_order_ele и AZ_transform. |
| extern_proc |
extern_proc[i] есть процессор, модифицирующий элемент external[i].
Образование массива и установку его значений выполняет функция AZ_find_procs_for_externs. |
| external |
Отсортированный список (глобальные индексы) внешних элементов на этом
процессоре. Образование списка и установку его значений выполняют функции
AZ_find_local_indices и AZ_transform. |
| N_external |
Число external компонент. Установку его значения выполняют функции
AZ_find_procs_for_externs и AZ_transform. |
| N_update |
Число update компонент. Установку его значения выполняет функция
AZ_read_update. |
| options, params |
Массивы, описывающие опции функции AZ_solve (раздел 2). |
| proc_config[AZ_node] |
Узловой идентификатор (номер) данного процессора. |
| proc_config[AZ_N_procs] |
Общее число процессоров, используемых выполняемой программой. Образует
и устанавливает значение функция AZ_processor_info. |
| update_index |
update_index[i] дает локальную нумерацию глобального элемента
update[i]. Образование массива и установку его значений выполняют
функции AZ_order_ele и AZ_transform. |
| update |
Отсортированный список элементов (глобальные индексы), которые должны
модифицироваться на этом процессоре. Образование списка и установку его
значений выполняет функция AZ_read_update. |
| val, bindx, bpntr, cpntr, indx, rpntr |
Массивы, используемые для хранения матрицы. Для MSR матриц массивы
bpntr, cpntr, indx, rpntr игнорируются (раздел 3). |
Прототип ______________________________________________________
void AZ_broadcast(char *ptr, int length, int *proc_config,
int action)
Описание _______
Конкатенирует буфер информации (т.е. добавляет информацию в буфер) и
распространяет эту информацию из процессора 0 в другие процессоры. Возможны
четыре действия:
- action == AZ_PACK
| - proc_config[AZ_node] == 0: |
сохранить ptr во внутреннем буфере. |
| - proc config[AZ_node] <> 0: |
считать из внутреннего буфера в ptr. Если внутренний буфер пустой,
он сначала получает распространяемую информацию. |
- action == AZ_SEND
| - proc_config[AZ_node] == 0: |
распространить внутренний буфер (наполненный функцией AZ_broadcast),
затем очистить его. |
| - proc_config[AZ_node] <> 0: |
очистить внутренний буфер. |
Образец применения:
Следующий фрагмент программы распространяет информацию в `a' и `b'.
if (proc_config[AZ_node] == 0) {
a = 1;
b = 2;
}
AZ_broadcast(&a, sizeof(int), proc_config, AZ_PACK);
AZ_broadcast(&b, sizeof(int), proc_config, AZ_PACK);
AZ_broadcast(NULL, 0 , proc_config, AZ_SEND);
ЗАМЕЧАНИЕ: Не может быть других коммуникационных вызовов между AZ_PACK
и AZ_SEND вызовами AZ_broadcast.
Параметры ______
| ptr |
Входной: строка данных размера length. Информация или сохраняется
в ptr, или рассылается из нее как описано выше. |
| length |
Входной: длина ptr (рассылаемой или получаемой). |
| action |
Входной: определяет поведение AZ_broadcast. |
Функции Aztec'а
Прототип ______________________________________________________
int AZ_check_input(int *data_org, int *options, double *params,
int *proc_config)
Описание _______
Выполняет проверки для итерационного решателя библиотеки. Вызывается
пользователем до вызова решателя, чтобы проверить значения в data_org,
options, params и proc_config. Если все значения верны, AZ_check_input
возвращает 0, иначе возвращает код ошибки, который может быть расшифрован
с помощью AZ_print_error.
Функции Aztec'а
Прототип ______________________________________________________
void AZ_check_msr(int *bindx, int N_update, int N_external,
int option, int *proc_config)
Описание _______
Прооверяет число ненулевых недиагональных элементов в каждой строке
и что индексы столбцов являются неотрицательными и не слишком большими
числами (см. option).
Параметры ______
option
|
AZ_LOCAL
|
Входной: указывает, что матрица использует локальные индексы. Число
ненулевых элементов в строке и наибольший индекс столбца не должны превышать
общее число элементов на этом процессоре.
|
|
AZ_GLOBAL
|
Входной: указывает, что матрица использует глобальные индексы. Число
ненулевых элементов в строке и наибольший индекс столбца не должны превышать
общее число элементов в моделировании.
|
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_check_vbr( |
int N_update, int N_external , int option,
int *bindx, int *bpntr , int *cpntr, int *rpntr,
int *proc_config ) |
Описание _______
VBR матрица проверяется на следующее:
- число столбцов внутри каждого блочного столбца неотрицательно.
- rpntr[i] == cpntr[i] для i =< N_update.
- число ненулевых блоков в каждой блочной строке неотрицательно и не
слишком большое.
- индексы блочного столбца неотрицательны и не слишком большие.
Параметры ______
option
|
AZ_LOCAL
|
Входной: указывает, что матрица использует локальные индексы. Число
ненулевых блоков в строке и наибольший индекс блочного столбца не должны
превышать общее число блочных столбцов на этом процессоре.
|
|
AZ_GLOBAL
|
Входной: указывает, что матрица использует глобальные индексы. Число
ненулевых блоков в строке и наибольший индекс блочного столбца не должны
превышать общее число блочных столбцов в моделировании.
|
Функции Aztec'а
Прототип ______________________________________________________
int AZ_defaults(int *options, double *params )
Описание _______
Установка options и params в значения по умолчанию.
Параметры ______
| options |
На выходе: установлены значения опций по умолчанию. |
| params |
На выходе: установлены значения параметров по умолчанию. |
Функции Aztec'а
Прототип ______________________________________________________
void AZ_exchange_bdry(double *x, int *data_org)
Описание _______
Локальная замена компонентов вектора x, при которой external компоненты
x модифицируются.
Параметры ______
| x |
На входе: вектор, определенный на этом процессоре. На выходе: external
компоненты x модифицированы через коммуникацию. |
Функции Aztec'а
Прототип ______________________________________________________
int AZ_find_index(int key, int *list, int length )
Описание _______
Возвращает индекс i в list (список должен быть отсортирован), который
соответствует ключу (т.е. list[i] == key). Если key не найден, AZ_find_index
возвращает -1. См. также AZ_quick_find.
Параметры ______
| key |
Входной: элемент, который ищется в списке. |
| list |
Входной: просматриваемый отсортированный список. |
| length |
Входной: длина списка. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_find_local_indices( |
int N_update, int *bindx, int *update, int
**external, int *N_external, int mat_type, int *bpntr
) |
Описание _______
По глобальным индексам столбцов матрицы и списку элементов, модифицируемых
на этом процессоре, вычисляет множество external и заменяет глобальные
индексы столбца локальными индексами столбца. Подробнее:
- образует external, вычисляет внешние компоненты и сохраняет в external.
- перенумеровывает индексы столбца так, что номер столбца k заменяется
на j, где либо update[j] == k, либо external[j - N_update] == k.
Вызывается функцией AZ_transform.
Параметры ______
| mat_type |
Входной: указывает, является ли матричный формат форматом MSR (= AZ_MSR_MATRIX)
или VBR (= AZ_VBR_MATRIX). |
| external |
Выходной: образовано множество и заполнено отсортированным списком
внешних элементов. |
| bindx |
На входе содержит глобальные номера столбцов MSR или VBR матрицы (раздел
3). На выходе содержит локальные номера столбцов (см. выше). |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_find_procs_for_externs( |
int N_update, int *update, int *external, int
N_external, int *proc_config, int **extern_proc) |
Описание _______
Определяет, какие процессоры ответственны за модифицирование каждого
внешнего элемента. Вызывается функцией AZ_transform.
Параметры ______
| extern_proc |
|
На выходе extern_proc[i] содержит узловой номер процессора,
который модифицирует external[i]. |
Функции Aztec'а
Прототип ______________________________________________________
void AZ_free_memory(int name)
Описание _______
Освобождает память Aztec'а, связанную с матрицами, у которых data_org[AZ_name]
= name. Это прежде всего информация о масштабировании и переобуславливании,
которая была вычислена предшествующими обращениями к AZ_solve.
Параметры ______
| name |
|
На выходе: вся информация о масштабировании и переобуславливании освобождается
для матриц, у которых data_org[AZ name] = name |
Функции Aztec'а
Прототип ______________________________________________________
double AZ_gavg_double(double value, int *proc_config )
Описание _______
Возвращает среднее значение чисел value на всех процессорах.
Параметры ______
| value |
|
Входной: value содержит значение двойной точности. |
Функции Aztec'а
Прототип ______________________________________________________
double AZ_gdot(int N, double *r, double *z, int *proc_config)
Описание _______
Возвращает скалярное произведение r и z с единичным шагом. Эта программа
вызывает BLAS-программу ddot для выполнения локального векторно-скалярного
произведения, а затем использует программу глобального суммирования AZ_GSUM_DOUBLE
для получения требуемого глобального результата.
Параметры ______
| N |
|
Входной: длина r и z на этом процессоре. |
| r, z |
|
Входные: векторы, распределенные по всем процессорам. |
Функции Aztec'а
Прототип ______________________________________________________
double AZ_gmax_double(double value, int *proc_config )
Описание _______
Возвращает максимум из чисел value на всех процессорах.
Параметры ______
| value |
|
Входной: value содержит число двойной точности. |
Функции Aztec'а
Прототип ______________________________________________________
int AZ_gmax_int(int value, int *proc_config )
Описание _______
Возвращает максимум из целых чисел value на всех процессорах.
Параметры ______
| value |
|
Входной: value содержит целое число. |
Функции Aztec'а
Прототип ______________________________________________________
| double AZ_gmax_matrix_norm( |
double *val, int *indx, int *bindx, int *rpntr,
int *cpntr, int *bpntr, int *proc_config, int *data_org) |
Описание _______
Возвращает максимальную матричную норму  для распределенной матрицы, закодированной в val, indx, bindx, rpntr, cpntr,
bpntr (раздел 3).
для распределенной матрицы, закодированной в val, indx, bindx, rpntr, cpntr,
bpntr (раздел 3).
Функции Aztec'а
Прототип ______________________________________________________
double AZ_gmax_vec(int N , double *vec, int *proc_config
)
Описание _______
Возвращает максимум всех чисел, размещенных в vec[i] (i < N ) на
всех процессорах.
Параметры ______
| vec |
|
Входной: vec содержит список чисел. |
| N |
|
Входной: длина vec. |
Функции Aztec'а
Прототип ______________________________________________________
double AZ_gmin_double(double value, int *proc_config )
Описание _______
Возвращает минимум из чисел value на всех процессорах.
Параметры ______
| value |
|
Входной: value содержит число двойной точности. |
Функции Aztec'а
Прототип ______________________________________________________
int AZ_gmin_int(int value, int *proc_config )
Описание _______
Возвращает минимум из целых чисел value на всех процессорах.
Параметры ______
| value |
|
Входной: value содержит целое число. |
Функции Aztec'а
Прототип ______________________________________________________
double AZ_gsum_double(double value, int *proc_config )
Описание _______
Возвращает сумму чисел value на всех процессорах.
Параметры ______
| value |
|
Входной: value содержит число двойной точности. |
Функции Aztec'а
Прототип ______________________________________________________
int AZ_gsum_int(int value, int *proc_config )
Описание _______
Возвращает сумму целых чисел value на всех процессорах.
Параметры ______
| value |
|
Входной: value содержит целое число. |
Функции Aztec'а
Прототип ______________________________________________________
void AZ_gsum_vec_int(int *values, int *wkspace, int length,
int *proc_config )
Описание _______
values[i] получает значение, равное сумме чисел values[i] на входе
на всех процессорах (i < length).
Параметры ______
| values |
|
На входе values содержит список целых чисел. На выходе values[i]
содержит сумму исходных values[i] на всех процессорах. |
| wkspace |
|
Входной: рабочий массив размера length. |
| length |
|
Входной: длина values и wkspace. |
Функции Aztec'а
Прототип ______________________________________________________
double AZ_gvector_norm(int n, int p, double *x , int
*proc_config )
Описание _______
Возвращает p норму вектора x, распределенного по процессорам:
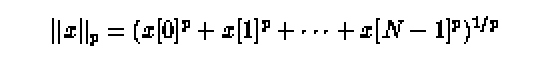
где N есть общее число элементов в x по всем процессорам.
ЗАМЕЧАНИЕ: Для нормы  полагаем
p= - 1.
полагаем
p= - 1.
Параметры ______
| n |
|
Входной: число update компонент x на этом процессоре. |
| p |
|
Входной: порядок вычисляемой нормы, т.е. 
|
| x |
|
Входной: вектор, норма которого вычисляется |
Функции Aztec'а
Прототип ______________________________________________________
void AZ_init_quick_find(int *list, int length, int *shift,
int *bins )
Описание _______
shift и bins задаются так, чтобы они могли использоваться в AZ_quick_find.
На выходе shift удовлетворяет
 и
и 
где range = list[length - 1] - list[0] . Массив bins должен быть размера
2 + length/4 и заполнен такими значениями, что

где  .
.
Эта программа используется вместе с AZ_quick_find. Идея состоит в том,
чтобы использовать bins для получения хорошего начального предположения
относительно расположения value в list.
Параметры ______
| list |
|
Входной: отсортированный list. |
| length |
|
Входной: длина list. |
| shift |
|
На выходе shift имеет значения, как описано выше. |
| bins |
|
На входе массив размера 2 + length/4. На выходе bins
имеет значения, как описано выше. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_invorder_vec( |
double *x, int *data_org, int *update_index,
int *rpntr , double *untrans_x ) |
Описание _______
Обратное преобразование вектора x, в котором расположение данных соответствует
преобразованной матрице (см. AZ_transform или AZ._reorder_matrix), так
что новый вектор (untrans_x) соответствует данным в первоначально заданном
пользователем порядке.
Параметры ______
| x |
Входной: распределенный вектор, в котором расположение данных соответствует
преобразованной матрице. |
| untrans_x |
Выходной: результат обратного преобразования x, так что расположение
данных теперь соответствует первоначальному порядку, заданному пользователем. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_matvec_mult( |
double *val, int *indx, int *bindx, int *rpntr,
int *cpntr, int *bpntr, double *b, double *c,
int exchange_flag, int *data_org ) |
Описание _______
Выполняет матрично-векторное умножение

где матрица А закодирована в val, indx, bindx, rpntr, cpntr, bpntr (раздел
3).
Параметры ______
| b |
Входной: распределенный вектор, участвующий в умножении. ЗАМЕЧАНИЕ:
b должен содержать data_org[AZ_N_internal]
+ data_org[AZ_N_border] + data_org[AZ_N_external]
элементов (хотя внешние переменные, хранимые в конце вектора, нет надобности
инициализировать). |
| c |
Выходной: результат матрично-векторного умножения. ЗАМЕЧАНИЕ: c
должен содержать data_org[AZ_N_internal] + data_org[AZ_N_border]
элементов. |
| exchange_flag |
Входной: определяет, нужна ли коммуникация. Если exchange_flag==
1, коммуникация нужна. Если exchange_flag == 0, то не нужна. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_msr2vbr( |
double *val, int *indx, int *rpntr, int *cpntr,
int *bpntr, int *bindx, int *bindx2, double *val2,
int total_blk_rows, int total_blk_cols, int blk_space,
int nz_space, int blk_type) |
Описание _______
Конвертирует DMSR матрицу, определенную в (val2, bindx2), в DVBR матрицу,
определенную в (val, indx, rpntr, cpntr, bpntr, bindx).
Параметры ______
| val2, bindx2 |
На выходе: DMSR массивы, содержащие матрицу, которая должна конвертироваться. |
| cpntr |
На входе: cpntr[i] есть размер i-го блока в результирующей
DVBR матрице. Столбцы с 0-го по cpntr[0] - 1 формируют первый блочный
столбец, Столбцы с cpntr[0] по cpntr[1] - 1 формируют второй
блочный столбец, и т.д. На выходе cpntr соответствует результирующей
DVBR матрице. |
val, indx, rpntr,
bpntr, bindx |
На выходе: DVBR массивы конвертированной DMSR матрицы. |
| total_blk_rows |
Входной: число блочных строк в результирующей локальной VBR матрице. |
| total_blk_cols |
Входной: число блочных столбцов в результирующей локальной VBR матрице. |
| blk_space |
Входной: длина, выделенная для bindx и indx. |
| nz_space |
Входной: длина, выделенная для val. |
| blk_type |
Входной: если blk_type > 0, то все блочные строки (и столбцы)
имеют тот же самый размер, заданный в blk_type. Если blk_type
< 0 , блочные строки имеют различные размеры. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_order_ele( |
int *update_index, int *extern_index, int *N_internal,
int *N_border, int N_update, int *bpntr, int *bindx,
int *extern_proc, int N_external, int option, int
mat_type) |
Описание _______
Упорядочивает update и external. Множество external упорядочивается
так, что элементы, модифицируемые одним и тем же процессором, располагаются
подряд. Если option == AZ_ALL, то update упорядочивается, причем internal
компоненты имеют наименьшие номера, за ними следуют border компоненты.
В противном случае порядок update не изменяется. Информация упорядочиввания
размещается в update_index и extern_index (раздел 4). Вызывается функцией
AZ_transform.
Параметры ______
| N_internal |
Выходной: число internal компонент на процессоре. |
| N_border |
Выходной: число border компонент на процессоре. |
| update_index |
Выходной: update_index[i] указывает локальный индекс (или порядок)
для update[i]. |
| extern_index |
Выходной: extern_index[i] указывает новый локальный индекс (или
порядок) для external[i]. |
| option |
Входной: указывает, переупорядочить ли update. |
|
AZ_ALL
|
|
|
AZ_EXTERNS
|
|
| mat_type |
Входной: указывает либо матричный формат MSR (= AZ_MSR_MATRIX),
либо VBR (= AZ_VBR_MATRIX). |
Функции Aztec'а
Прототип ______________________________________________________
void AZ_print_error(int error_code)
Описание _______
Выводит на печать сообщение об ошибке, соответствующее error_code. Обычно
error_code генерируется с помощью AZ_check_input.
Параметры ______
| error_code |
|
Входной: код ошибки, генерируемый AZ_check_input. |
|
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_print_out( |
int *update_index, int *extern_index, int *update,
int *external, double *val, int *indx, int *bindx,
int *rpntr, int *cpntr, int *bpntr, int *proc_config,
int choice, int matrix_type, int N_update, int N_external,
int offset ) |
Описание _______
Печатает Aztec матрицы в одном из нескольких форматов:
- choice = AZ_input_form
Вывод, соответствующий рисунку 4 (для VBR матриц информация похожа).
Матрица может быть напечатана или до, или после работы AZ_transform.
- choice = AZ_global_mat
Может использоваться только на матрицах, трансформированных AZ_transform.
Ненулевые элементы печатаются в виде:
- MSR: a(I + offset, J + offset) = value;
- VBR: a(I + offset(i), J + offset(j)) = value;
где I, J - глобальные индексы (блочных) строки и столбца, а i,
j - положение строки и столбца внутри блока.
- choice = AZ_explicit
Подобно AZ_global_mat за исключением интерпретации (I, J).
Если используется для трансформированных с помощью AZ_transform
матриц и вместо update передан NULL, то (I,J) являются
локальными строками и столбцами на этом процессоре. Если используется перед
AZ_transform и передано update, то (I,J) соответствуют
глобальной матричной нумерации.
ЗАМЕЧАНИЕ: update_index, extern_index, update, external и N_external
используется только для опции AZ_global_mat. Кроме того, если установлена
в NULL, то cpntr не печатается и не используется.
Параметры ______
| choice |
|
Входной: выбирает формат вывода (описаны выше). |
| matrix_type |
|
Входной: указывает либо матричный формат AZ_VBR_MATRIX, либо
AZ_MSR_MATRIX. |
| N_update |
|
Входной: число (блочных) строк, распределенных процессору. |
| N_external |
|
Входной: data_org[AZ_N_ext_blks]. |
| offset |
|
Входной: смещение строки и столбца. См. описание выше. |
Функции Aztec'а
Прототип ______________________________________________________
void AZ_processor_info(int *proc_config)
Описание _______
proc_config[AZ_node] становится равным узловому номеру данного
процессора. proc_config[AZ_N_proc] становится равным количеству
процессоров, используемых в вычислениях.
Функции Aztec'а
Прототип ______________________________________________________
int AZ_quick_find(int key, int *list, int length,
int shift, int *bins )
Описание _______
Возвращает индекс i в list (предполагается, что он отсортирован),
который соответствует ключу (т.е. list[i] = key). Если key
не найден, то AZ_quick_find возвращает -1.
ЗАМЕЧАНИЕ: Эта функция быстрее, чем AZ_find_index, но требует, чтобы
функция AZ_init_quick_find установила и сохранила bins.
| key |
|
Входной: искомый элемент в list. |
| list |
|
Входной: отсортированный список, в котором ведется поиск. |
| length |
|
Входной: длина списка. |
| shift |
|
Входной: используется для начального предположения (вычислен предыдущим
вызовом AZ_init_quick_find). |
| bins |
|
Входной: вычислен с помощью AZ_init_quick_find для начального
предположения. bins установлен так, что list[bins[k]] <= key
< list[bins[k + 1]], где k = (key - list[0])/2shift. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_read_msr_matrix( |
int *update, double **val, int **bindx, int
N_update, int *proc_config) |
Описание _______
Читает файл .data и создает матрицу в формате MSR. Чтение входного
файла выполняет процессор 0. Если очередная добавляемая строка находится
в update 0-ого процессора, то она добавляется к матрице этого процессора.
В противном случае процессор 0 определяет, какой процессор запросил эту
строку и посылает ее этому процессору для его локальной матрицы. Форма
входного файла следующая:
num_rows
col_num1 entry1 col_num2 entry2
col_num3 entry3 -1
col_num4 entry4 col_num5 entry5
col_num6 entry6 -1
Эти входные ланные соответствуют двум строкам: 0 и 1. Строка 0 содержит
entry1 в столбце col_num1, entry2 в столбце col_num2
и entry3 в столбце col_num3. Строка 1 содержит entry4
в столбце col_num4, entry5 в столбце col_num5 и entry6
в столбце col_num6. При использовании экспоненциального представления
чисел надо использовать `E' или `e' вместо `D' или `d'. Кроме того, номера
строк и столбцов должны нумероваться от 0 до n-l, а не от 1 до n, где n
есть число строк.
ЗАМЕЧАНИЕ: Пробел и возврат каретки не важны.
ЗАМЕЧАНИЕ: AZ_read_msr_matrix() неэффективна для больших матриц.
Эту программу, однако, можно использовать для чтения бинарных файлов. В
частности, если Aztec компилируется с -Dbinary опцией, `.data' должен
содержать двоичные целые числа и двоичные числа двойной точности в той
же самой описанной выше форме, за исключением пробелов или возвратов каретки
между числами. Так как двоичные форматы не являются стандартными, `.data'
должен быть создан C программой с помощью fread() и fwrite() на той же
машине, где установлен Aztec.
Параметры ______
| val, bindx |
|
|
На выходе: этим двум массивам выделено место и они заполнены в формате
MSR значениями, соответствующими файлу .data. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_read_update( |
int *N_update, int **update, int *proc_config,
int N , int chunk , int input_option ) |
Описание _______
Эта программа инициализирует update глобальными индексами, которые
модифицируются данным процессором, и заносит в N_update общее число
модифицируемых элементов.
Параметры ______
| N_update |
|
|
На выходе: число элементов, модифицируемых процессором. |
| update |
|
|
На выходе: update содержит список элементов в порядке возрастания,
модифицируемых этим процессором. |
| chunk |
|
|
Число индексов внутри группы. Например, chunk == 2 => chunk0
= {0, 1} и chunk1 = {2, 3}. |
| N |
|
|
Общее число кусков в векторе. |
| input_option |
|
AZ_linear
|
|
|
Процессору 0 назначаются первые  кусков, процессору 1 назначаются следующие
кусков, процессору 1 назначаются следующие  кусков и т.д.,
кусков и т.д.,
где P = proc_config[AZ_N_proc]).
|
|
AZ_box
|
|
|
Система процессоров рассматривается как массив p2
* p1 * p0, а матричной задаче соответствует
сетка n2 * n1 * n0
с неизвестными "кусками" в каждой точке сетки. Пользователь запрашивается
о значениях pi-ых и ni-ых. В предположении, что сетка
упорядочена "естественно", или лексикографически, она подразделяется
на однородные ячейки, чьи соответствующие строки должны назначаться каждому
процессору.
|
|
AZ_file
|
|
|
Читает proc_config[AZ_N_proc] списки, содержащиеся в файле .update.
Каждый список содержит множество глобальных индексов, перед которым стоит
число индексов в этом множестве. Список 0 посылается процессору proc_config[AZ_N_proc]
- 1, список 1 посылается процессору proc_config[AZ_N_proc] - 2,
и т.д. Замечание: Файлы в этом формате вырабатывает пакет разбиения графов,
называемый Chaco [2].
|
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_reorder_matrix( |
int N_update, int *bindx, double *val, int
*update_index, int *extern_index, int *indx, int *rpntr,
int *bpntr, int N_external, int *cpntr, int option,
int mat_type) |
Описание _______
Переупорядочивает матрицу в соответствии с новым порядком, заданным
в update_index и extern_index. А именно, индексы (update[i],
update[j]) элементов глобальной матрицы, которые хранились как индексы
(i, j) локальной матрицы, на выходе запоминаются как (update_index[i],
update_index[j]). Аналогично, индексы (update[i], external[k])
элементов глобальной матрицы, которые хранились как индексы (i, k +
N_update) локальной матрицы, на выходе запоминаются локально как (update_index[i],
extern_index[k]). Вызывается функцией AZ_transform. ВАЖНОЕ ЗАМЕЧАНИЕ:
Эта программа предполагает, что update_index содержит две последовательности
чисел, которые упорядочены, но переплетены. Например,
| update_index: |
|
4 |
5 |
0 |
6 |
1 |
2 |
3 |
7 |
| последовательность 1: |
|
|
|
0 |
|
1 |
2 |
3 |
|
| последовательность 2: |
|
4 |
5 |
|
6 |
|
|
|
7 |
См. также AZ_reorder_vec и AZ_invorder_vec для преобразования
правой части и вектора решения.
Параметры ______
| option |
Входной: указывает, упорядочивать ли изменяемые элементы: |
|
AZ_ALL
|
|
|
AZ_EXTERNS
|
Перенумеровываются только столбцы, соответствующие внешним элементам.
|
| mat_type |
Входной: указывает формат матрицы: |
|
AZ_MSR_MATRIX
|
|
|
AZ_VBR_MATRIX
|
|
| bindx, val, indx, rpntr, bpntr, cpntr |
На входе: матрица упорядочена, как описано выше. На выходе: матрица
переупорядочена с использованием update_index и extern_index,
как описано выше. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_reorder_vec( |
double *x, int *data_org, int *update_index,
int *rpntr ) |
Описание _______
Преобразовывает вектор x, размещение данных которого соответствует
заданному пользователем порядку (т.е. x[i] соответствует глобальному
векторному элементу x[update[i]]) таким образом, что теперь данные
соответствуют преобразованной матрице (см. AZ_transform или AZ._reorder_matrix).
Параметры ______
| x |
|
На входе: распределенный вектор, планировка данных которого соответствует
первоначально заданному пользователем порядку, На выходе: планировка данных
теперь соответствует преобразованной матрице, чье упорядочение задается
через update_index. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_set_message_info( |
int N_external, int *extern_index, int N_update,
int *external, int *extern_proc, int *update, int
*update_index, int *proc_config, int *cpntr, int **
data_org, int mat_type) |
Описание _______
Инициализирует data_org так, чтобы при выполнении матрично-векторных
произведений могла использоваться коммуникация. Это включает:
- определение соседей, от которых мы получаем или кому посылаем.
- определение общего числа элементов, которые мы посылаем, и образование
data_org.
- инициализация data_org как описано в разделе 6.1.
ЗАМЕЧАНИЕ: data_org[AZ_name] устанавливается в число
(начиная с 1), которое увеличивается при каждом вызове AZ_set_message_info.
Вызывается функцией AZ_transform.
ЗАМЕЧАНИЕ: Соседи неявно нумеруются, используя упорядочение внешних элементов
(которые были предварительно упорядочены так, что элементы, модифицируемые
одним и тем же процессором, являются смежными).
Параметры ______
| data_org |
Выходной: образуется data_org и полностью инициализируется как
описано в разделе 6.1. |
| mat_type |
Входной: указывает матричный формат: |
|
AZ_MSR_MATRIX
|
|
|
AZ_VBR_MATRIX
|
|
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_solve( |
double *x, double *b, int *options, double
*params, int *indx, int *bindx, int *rpntr,
int *cpntr, int *bpntr, double *val, int *data_org,
double *status, int *proc_config) |
Описание _______
Решение системы уравнений Ax = b итерационным методом, где матрица
A закодирована в indx, bindx, rpntr, cpntr, bpntr и val
(см. раздел 3 и раздел 2).
Параметры ______
| x |
x - начальное приближение на входе и решение системы на выходе.
ЗАМЕЧАНИЕ:x должен содержать data_org[AZ_N_internal] + data_org[AZ_N_border]
+ data_org[AZ_N_external] элементов (хотя внешние переменные, хранимые
в конце вектора, нет необходимости инициализировать). |
| b |
Вектор длины data_org[AZ_N_internal] + data_org[AZ_N_border],
содержащий правую часть. |
| options,params |
Опции и параметры, используемые в процессе решения (раздел 2). |
| status |
На выходе: состояние итерационного метода решения (раздел 2). |
Функции Aztec'а
Прототип ______________________________________________________
void AZ_sort(int *list1 , int N , int *list2 , double
*list3 )
Описание _______
Сортирует элементы в list1. Кроме того, перемещает элементы в
list2 и list3 так же, как они были перемещены в list1.
ЗАМЕЧАНИЕ: если list2 == NULL, то list2 не обрабатывается.
Если list3 == NULL, то list3 не обрабатывается.
Параметры ______
| list1 |
|
На входе: значения до сортировки. На выходе: отсортированные значения
(т.е. list1[i] <= list1[i+1]) |
| N |
|
На входе: длина сортируемых списков. |
| list2 |
|
На входе: список, связанный с list1. На выходе: если исходный
list1[k] сохраняется на выходе в list1[j], то исходный list2[k]
также сохраняется на выходе в list2[j]. |
| list3 |
|
На входе: список, связанный с list1. На выходе: если исходный
list1[k] сохраняется на выходе в list1[j], то исходный list3[k]
также сохраняется на выходе в list3[j]. Замечание: если на входе
list3 == NULL, он не изменяется на выходе. |
Функции Aztec'а
Прототип ______________________________________________________
| void AZ_transform( |
int *proc_config, int **external, int *bindx,
double *val, int *update, int **update_index, int
**extern_index, int **data_org, int N_update, int
*indx, int *bpntr, int *rpntr, int **cpntr,
int mat_type) |
Описание _______
Конвертирует описание глобальной матрицы в распределенный матричный
формат (см. раздел 2 и раздел 6.4). См. также AZ_reorder_vec и AZ_invorder_vec
для преобразования вектора правой части и вектора решения.
Параметры ______
| external |
На выходе: образован массив и установлен на компоненты, которые должны
передаваться при коммуникациях во время матрично-векторного умножения. |
| bindx, val, index, bpntr, rpntr |
На входе: массивы матриц (MSR или VBR), соответствующие глобальному
формату. На выходе: массивы матриц (DMSR или DVBR), соответствующие локальному
формату. См. раздел 2. |
| update_index |
На выходе: образован массив и установлен так, что update_index[i]
является локальной нумерацией, соответствующей update[i]. |
| extern_index |
На выходе: образован массив и установлен так, что extern_index[i]
является локальной нумерацией, соответствующей external[i]. |
| data_org |
На выходе: образован массив и установлена информация по планировке
данных. См. раздел 6.1. |
| cpntr |
На выходе: образован массив и установлен для VBR матриц указателями
столбца. |
| mat_type |
На входе: матричный формат (либо AZ_VBR_MATRIX, либо AZ_MSR_MATRIX). |
Функции Aztec'а
ЛИТЕРАТУРА
| [1] |
S. Carney, M. Heroux, and G. Li. A proposal for a sparse BLAS toolkit.
Technical report, Cray Research Inc., Eagen, MN, 1993. |
| [2] |
B. Hendrickson and R. Leland. The Chaco user's guide - version 1.0.
Technical Report Sand93-2339, Sandia National Laboratories, Albuquerque
NM, 87185, August 1993. |
| [3] |
J.N. Shadid and R.S. Tuminaro. Sparse iterative algorithm software
for large-scale MIMD machines: An initial discussion and implementation.
Concurrency: Practice and Experience, 4(6):481-497, September 1992. |
|
| [4] |
J.N. Shadid and R.S. Tuminaro. Aztec - a parallel preconditioned Krylov
solver library: Algorithm description version 1.0. Technical Report Sand95:in
preparation, Sandia National Laboratories, Albuquerque NM, 87185, August
1995. |
| [5] |
R.S. Tuminaro, J.N. Shadid, and S.A. Hutchinson. Parallel sparse matrix
vector multiply software for matrices with data locality. Submitted to
BIT, August 1995. |
| [6] |
Z.Zlatev, V.A. Barker, and P.G. Thomsen. SSLEST - a FORTRAN IV subroutine
for solving sparse systems of linear equations (user's guide). Technical
report, Institute for Numerical Analysis, Technical University of Denmark,
Lyngby,Denmark, 1978. |
![]()
![]()
![]()
![]()
![]() , где
, где  ,
n - общее число неизвестных, w - вес вектора, задаваемый
пользователем через params[AZ_weights] и
,
n - общее число неизвестных, w - вес вектора, задаваемый
пользователем через params[AZ_weights] и ![]() - начальная невязка.
- начальная невязка.![]() устанавливается в начальный
вектор невязки.
устанавливается в начальный
вектор невязки.![]() устанавливается в набор случайных
чисел между -1 и 1. ЗАМЕЧАНИЕ: При использовании этой опции сходимость
зависит от числа процессоров (т.е. итерации, полученные на x процессорах,
отличаются от итераций, полученных на у процессорах, если x
не равно y).
устанавливается в набор случайных
чисел между -1 и 1. ЗАМЕЧАНИЕ: При использовании этой опции сходимость
зависит от числа процессоров (т.е. итерации, полученные на x процессорах,
отличаются от итераций, полученных на у процессорах, если x
не равно y).