 ,
nis the total number of unknowns, w is a weight vector provided
by the user via params[AZ_weights] and
,
nis the total number of unknowns, w is a weight vector provided
by the user via params[AZ_weights] and
Scott A. Hutchinson(y) John N. Shadid(x) Ray S.
Tuminaro(z)
Massively Parallel Computing Research Laboratory
Sandia National Laboratories
Albuquerque, NM 87185
Aztec is an iterative library that greatly simplifies the parallelization
process when solving the linear systems of equations Ax = b where
A is a user supplied n * n sparse matrix, b is a user supplied
vector of length n and x is a vector of length n to
be computed. Aztec is intended as a software tool for users who
want to avoid cumbersome parallel programming details but who have large
sparse linear systems which require an efficiently utilized parallel processing
system. A collection of data transformation tools are provided that allow
for easy creation of distributed sparse unstructured matrices for parallel
solution. Once the distributed matrix is created, computation can be performed
on any of the parallel machines running Aztec: nCUBE 2, IBM SP2
and Intel Paragon, MPI platforms as well as standard serial and vector
platforms.
Aztec includes a number of Krylov iterative methods such as conjugate
gradi ent (CG), generalized minimum residual (GMRES) and stabilized biconjugate
gradient (BiCGSTAB) to solve systems of equations. These Krylov methods
are used in conjunction with various preconditioners such as polynomial
or domain decomposition methods using LU or incomplete LU factorizations
within subdomains. Although the matrix A can be general, the package has
been designed for matrices arising from the approximation of partial differential
equations (PDEs).
______
*This work was supported by the Applied Mathematical Sciences program,
U.S. Department of Energy, Office of Energy Research, and was performed
at Sandia National Laboratories, operated for the U.S. Department of Energy
under contract No. DE-AC04-94AL85000. The Aztec software package
was developed by the authors at Sandia National Laboratories and is under
copyright protection
y Parallel Computational Sciences Department; sahutch@cs.sandia.gov; (505)
845-7996
x Parallel Computational Sciences Department; jnshadi@cs.sandia.gov; (505)
845-7876
z Applied & Numerical Mathematics Department; tuminaro@cs.sandia.gov;
(505) 845-7298
Contents.
2 Aztec:High Level View
2.1 Aztec Options
2.2 Aztec parameters
2.3 Return status
3 Data Formats
3.1
Distributed Modified Sparse Row (DMSR) Format
3.2 Distributed
Variable Block Row (DVBR) Format
4 High Level Data Interface
5 Examples
6 Advanced Topics
6.1 Data Layout
6.2 Reusing factorizations
6.3 Important Constants
6.4 AZ_transform Subtasks
7 Aztec Functions
AZ_broadcast
AZ_check_input
AZ_check_msr
AZ_check_vbr
AZ_defaults
AZ_exchange_bdry
AZ_find_index
AZ_find_local_indices
AZ_find_procs_for externs
AZ_free_memory
AZ_gavg_double
AZ_gdot
AZ_gmax_double
AZ_gmax_int
AZ_gmax_matrix_norm
AZ_gmax_vec
AZ_gmin_double
AZ_gmin_int
AZ_gsum_double
AZ_gsum_int
AZ_gsum_vec int
AZ_gvector_norm
AZ_init_quick_find
AZ_invorder_vec
AZ_matvec_mult
AZ_msr2vbr
AZ_order_ele
AZ_print_error
AZ_print_out
AZ_processor_info
AZ_quick_find
AZ_read_msr_matrix
AZ_read_update
AZ_reorder_matrix
AZ_reorder_vec
AZ_set_message_info
AZ_solve
AZ_sort
AZ_transform
Notation Conventions
Different fonts are used to indicate program fragments, keys words,
variables, or
parameters in order to clarify the presentation. The table below describes
the
meaning denoted by these different fonts.
Convention Meaning
| typewriter | File names, code examples and code fragments. |
| sans serif | C language elements such as function names and constants when they appear embedded in text or in function definition syntax lines. |
| italics | Parameter and variable names when they appear embedded in text or function definition syntax lines. |
| AZ_ | C language elements such as function names and constants which are supplied by the Aztec library. |
Code Distribution
Aztec is publicly available for research purposes and may be licensed
for commercial application. The code is distributed along with technical
documentation, example C and Fortran driver routines and sample input files
via the internet. It may be obtained by contacting one of the authors listed
on page i of this report.
1. Overview. Aztec is an iterative library
that greatly simplifies the parallelization process when solving the linear
system of equations
Ax = b where A is a user supplied n * n sparse matrix,
b is a user supplied vector of length n and x is a vector
of length n to be computed. Aztec is intended as a software
tool for users who want to avoid cumbersome parallel programming details
but who have large sparse linear systems requiring efficient use of a parallel
processing system. The most complicated parallelization task for an Aztec
user is the distributed matrix specification for the particular application.
Although this may seem difficult, a collection of data transformation tools
are provided that allow creation of distributed sparse unstructured matrices
for parallel solution with ease of effort that is similar to a serial implementation.
Background information regarding the data transformation tools can be found
in [5]. Once the distributed matrix is created, computation can occur on
any of the parallel machines running Aztec: nCUBE 2, IBM SP2, Intel
Paragon, and MPI platforms. In addition, Aztec can be used on standard
serial and vector platforms such as SUN, SGI and CRAY computers.
Aztec includes a number of Krylov iterative methods such as conjugate
gradi ent (CG), generalized minimum residual (GMRES) and stabilized biconjugate
gradient (BiCGSTAB) to solve systems of equations. These Krylov methods
are used in con junction with various preconditioners such as polynomial
preconditioners or domain decomposition using LU or incomplete LU factorizations
within subdomains. Back ground information concerning the iterative methods
and the preconditioners can be found in [4]. Although the matrix A can
be general, the package has been designed for matrices arising from the
approximation of partial differential equations (PDEs). In particular,
the preconditioners, iterative methods and parallelization techniques are
oriented toward systems arising from PDE applications. Lastly, Aztec
can use one of two different sparse matrix notations - either a point-entry
modified sparse row (MSR) format or a block-entry variable block row (VBR)
format. These two formats have been generalized for parallel implementation
and, as such, are referred to as "distributed" yielding DMSR
and DVBR references.
The remainder of this guide describes how Aztec is invoked within
an application. Aztec is written in ANSI-standard C and as such,
all arrays in the descriptions which follow begin indexing with 0. Also,
all function prototypes (loosely, descriptions) are presented in ANSI C
format. Section 2 discusses iterative method, preconditioning and convergence
options. Section 3 explains vectors and sparse matrix formats supported
by Aztec. In Section 4 we discuss the data transformation tool for
creating distributed vectors and matrices. A concrete detailed programming
example using this tool is given in Section 5 and some advance topics are
discussed in Section 6. Finally, Section 7 gives a glossary of Aztec
functions available to users.
contents
2. Aztec: High Level View.The
following tasks must be performed to success fully invoke Aztec:
* describe the parallel machine (e.g. number of processors).
* initialize matrix and vector data structures.
* choose iterative methods, preconditioners and the convergence criteria.
* initialize the right hand side and initial guess.
* invoke the solver.
Example________________________________________________________
#include "az_aztec.h"
void main(void) {
AZ_processor_info(proc_config);
init_matrix_vector_structures(bindx, val, update, external,update_index,
extern_index, data_org);
init_options(options, params);
init_guess_and_rhs(x, b, data_org, update, update_index);
AZ_solve(x, b, options, params, bindx, val, data_org, status,proc_config);
}
Fig. 1. High level code forAztec application. A sample
C program is shown in Figure 1 omitting declarations and some parameters
(1). The functions init_matrix_vector_structures, init_options, and init_guess_and_rhs
are supplied by the user. In this section, we give an overview of Aztec's
features by describing the user input arrays, options and params,
that are set by the user in the function init options. A discussion of
the other subroutines is deferred to Sections 4 and 5.
2.1. Aztec Options. options
is an integer array of length AZ_OPTIONS_SIZE se by the user. It is used
(but not altered) by the function AZ_solve to choose between iterative
solvers, preconditioners, etc. Below we discuss each of the possible options.
In some of these descriptions, reference is made to a user-defined options
or params value which is yet be introduced. These descriptions will
follow but the reader may wish to "jump ahead" and read the descriptions
if the immediate context is not clear.
Specifications_________________________________________________________________
| options[AZ_solver] | Specifies solution algorithm. DEFAULT: AZ_gmres. |
| AZ_cg | Conjugate gradient (only applicable to symmetric positive definite matrices). |
| AZ_gmres | Restarted generalized minimal residual. |
| AZ_cgs | Conjugate gradient squared. |
| AZ_tfqmr | Transpose-free quasi-minimal residual. |
| AZ_bicgstab | Bi-conjugate gradient with stabilization. |
| AZ_lu | Sparse direct solver (single processor only). |
| options[AZ_scaling] | Specifies scaling algorithm. The entire matrix is scaled (overwriting the old matrix). Additionally, the right hand side, the initial guess and the final computed solution are scaled if necessary. DEFAULT:AZ_none. |
| AZ_none | No scaling. |
| AZ_Jacobi | Point Jacobi scaling. |
| AZ_BJacobi | Block Jacobi scaling where the block size corre sponds to the VBR blocks. Point Jacobi scaling is performed when using the MSR format. |
| AZ_row_sum | Scale each row so the magnitude of its elements sum to 1. |
| AZ_sym_diag | Symmetric scaling so diagonal elements are 1. |
| AZ_sym_row_sum | Symmetric scaling using the matrix row sums. |
| options[AZ_precond] | Specifies preconditioner. DEFAULT:AZ_none. |
| AZ_none | No preconditioning. |
| AZ_Jacobi | k step Jacobi (block Jacobi for DVBR matrices where each block corresponds to a VBR block). The number of Jacobi steps, k, is set via options[AZ_poly_ord] . |
| AZ_Neumann | Neumann series polynomial where the polynomial order is set via options[AZ_poly_ord] . |
| AZ_ls | Least-squares polynomial where the polynomial order is set via options[AZ_poly_ord] . |
| AZ_lu | Domain decomposition preconditioner (additive Schwarz) using a sparse LU factorization in conjunction with a drop tolerance params[AZ_drop] on each processor's submatrix. The treatment of external variables in the submatrix is determined by options[AZ_overlap] . The current sparse lu factorization is provided by the package y12m [6]. |
| AZ_ilu | Similar to AZ_lu using ilu(0) instead of LU. |
| AZ_bilu | Similar to AZ_lu using block ilu(0) instead of LU where each block corresponds to a VBR block. |
| AZ_sym_GS | Non-overlapping domain decomposition (additive Schwarz) k step symmetric Gauss-Siedel. In par ticular, a symmetric Gauss-Siedel domain decom position procedure is used where each processor independently performs one step of symmetric Gauss-Siedel on its local matrix, followed by com munication to update boundary values before the next local symmetric Gauss-Siedel step.The num ber of steps, k, is set via options[AZ_poly_ord] . |
| options[AZ_conv] | Determines the residual expression used in convergence checks and printing. DEFAULT: AZ_r0. The iterative solver terminates if the corresponding residual expres sion is less than params[AZ_tol]: |
| AZ_r0 | |
| AZ_rhs | |
| AZ_Anorm | |
| AZ_sol | |
| AZ_weighted |  ,
nis the total number of unknowns, w is a weight vector provided
by the user via params[AZ_weights] and ,
nis the total number of unknowns, w is a weight vector provided
by the user via params[AZ_weights] and |
| options[AZ_output] | Specifies information (residual expressions - seeoptions[AZ_conv]
) to be printed. DEFAULT: 1. |
| AZ_all | Print out the matrix and indexing vectors for each processor. Print
out all intermediate residual express ions. |
| AZ_none | No intermediate results are printed. |
| AZ_warnings | Only Aztec warnings are printed. |
| AZ_last | Print out only the final residual expression. |
| >0 | Print residual expression every options[AZ_output] iterations. |
| options[AZ_pre_calc] | Indicates whether to use factorization information from previous calls to AZ_solve. DEFAULT:AZ_calc. |
| AZ_calc | Use no information from previous AZ_solve calls. |
| AZ_recalc | Use preprocessing information from a previous call but recalculate preconditioning factors. This is primarily intended for factorization software which performs a symbolic stage. |
| AZ_reuse | Use preconditioner from a previous AZ_solve call, do not recalculate preconditioning factors. Also, use scaling factors from previous call to scale the right hand side, initial guess and the final solution. |
| options[AZ_max_iter] | Maximum number of iterations. DEFAULT: 500. |
| options[AZ_poly_ord] | The polynomial order when using polynomial precondi tioning. Also, the number of steps when using Jacobi or symmetric Gauss-Seidel preconditioning. DEFAULT: 3. |
| options[AZ_overlap] | Determines the submatrices factored with the domain decomposition algorithms: AZ_lu, AZ_ilu, AZ_bilu. DEFAULT: AZ_none. |
| AZ_none | Factor the local submatrix defined on this proces sor discarding column entries that correspond to external elements. |
| AZ_diag | Factor the local submatrix defined on this pro cessor augmented by a diagonal (block diagonal for VBR format) matrix. This diagonal matrix corresponds to the diagonal entries of the matrix rows (found on other processors) associated with external elements. This can be viewed as taking one Jacobi step to update the external elements and then performing domain decomposition with AZ_none on the residual equations. |
| AZ_full | Factor the local submatrix defined on this proces sor augmented by the rows (found on other proces sors) associated with external variables (discard ing column entries associated with variables not defined on this processor). The resulting proce dure is an overlapped additive Schwarz procedure. |
| options[AZ_kspace] | Krylov subspace size for restarted GMRES. DEFAULT: 30. |
| options[AZ_orthog] | GMRES orthogonalization scheme. DEFAULT: AZ_classic. |
| AZ_classic | Classical Gramm-Schmidt orthogonalization. |
| AZ_modified | Modified Gramm-Schmidt orthogonalization. |
| options[AZ_aux_vec] | Determines ~r (a required vector within some iterative methods). The convergence behavior varies slightly de pending on how this is set. DEFAULT: AZ_resid. |
| AZ_resid | |
| AZ_rand | NOTE: When using this option, the convergence depends on the number of processors (i.e. the iterates obtained with x processors differ from the iterates obtained with y processors if x # y). |
2.2. Aztec parameters. params
is a double precision array set by the user and normally of length AZ_PARAMS_SIZE.
However, when a weight vector is needed for the convergence check (i.e.
options[AZ_conv] = AZ_weighted), it is embedded in params
whose length must now be AZ_PARAMS_SIZE + # of elements updated on this
proces sor. In either case, the contents of params are used (but
not altered) by the function AZ_solve to control the behavior of the iterative
methods. The array elements are specified as follows:
Specifications__________________________________________________
| params[AZ_tol] | Specifies tolerance value used in conjunction with convergence tests.
DEFAULT: 0.0000001 |
| params[AZ_drop] | Specifies drop tolerance used in conjunction with LU preconditioner. DEFAULT: 0.0. |
| params[AZ_weights] | When options[AZ_conv] = AZ_weighted, the i 'th local component of the weight vector is stored in the location params[AZ_weights+i]. |
Figure 2 illustrates a sample function init_options where the Aztec
function AZ_defaults sets the default options.
2.3. Return status. status
is a double precision array of length AZ_STATUS_SIZE returned from AZ_solve
( All integer information returned from AZ_solve is cast
into double precision and stored in status.). The contents
of status are described below.
Specifications__________________________________________________
| status[AZ_its] | Number of iterations taken by the iterative method. |
| status[AZ_why] | Reason why AZ_solve terminated. |
| AZ_normal | User requested convergence criteria is satisfied. |
| AZ_param | User requested option is not available. |
| AZ_breakdown | Numerical breakdown occurred. |
| AZ_loss | Numerical loss of precision occurred. |
| AZ_ill_cond | The Hessenberg within GMRES is ill-conditioned. This could be caused by a singular application matrix. In this case, GMRES tries to compute a least-squares solution. |
| AZ_maxits | Maximum iterations taken without convergence. |
| status[AZ_r] | The true residual norm corresponding to the choice options[AZ_conv] (this norm is calculated using the computed solution). |
| status[AZ_scaled_r] | The true residual ratio expression as defined by options[AZ_conv]. |
| status[AZ_rec_r] | Norm corresponding to options[AZ_conv] of final resid ual or estimated final residual (recursively computed by iterative method). Note: When using the 2-norm, tfqmr computes an estimate of the residual norm in stead of computing the residual. |
Example_____________
void init_options(int options[AZ_OPTIONS_SIZE],
double params[AZ_PARAMS_SIZE])
{
AZ_defaults(options,params);
| options[AZ_solver] | = AZ_cgs; |
| options[AZ_scaling] | = AZ_none; |
| options[AZ_precond] | = AZ_ls; |
| options[AZ_output] | = 1; |
| options[AZ_max_iter] | = 640; |
| options[AZ_poly_ord] | = 7; |
| params[AZ_tol] | = 0.0000001; |
}
Fig. 2.Example option initialization routine ( init_options).
When AZ_solve returns abnormally, the user may elect to restart using
the current computed solution as an initial guess.
contents
3. Data Formats. In this section
we describe the matrix and vector formats used internally by Aztec.
In Section 4 we discuss a tool that transforms data from a simpler format
to this format. Here, the terms "element" and "component"
are used inter changeably to denote a particular entry of a vector.
The sparse matrix-vector product, y <- Ax, is the major kernel operation
of Aztec.
To perform this operation in parallel, the vectors x and y
as well as the matrix A must be distributed across the processors. The
elements of any vector of length n are assigned to a particular processor
via some partitioning method (e.g. Chaco [2]). When calculating
elements in a vector such as y, a processor computes only those
elements in y which it has been assigned. These vector elements are explicitly
stored on the processor and are defined by a set of indices referred to
as the processor's update set. The update set is further
divided into two subsets: internal and border. A component
corresponding to an index in the internal set is updated using only
information on the current processor. As an example, the index i
is in internal if, in the matrix-vector product kernel, the element
yi is updated by this processor and if each j defining a
nonzero Aij in row i is in update. The border
set defines elements which would require values from other processors in
order to be updated during the matrix vector product. For example, the
index i is in border if, in the matrix-vector product kernel,
the element yi is updated by this processor and if there exists
at least one j associated with a nonzero Aij found in row i that
is not in update. In the matrix-vector product, the set of indices
which identify the off-processor elements in x that are needed to update
components corresponding to border indices is referred to as
external. They are explicitly stored by and are obtained from other
processors via communication whenever a matrix-vector product is performed.
Figure 3 illustrates how a set of vertices in a partitioning of a grid
would be used to define these sets. Since these sets of indices are used
exclusively

to reference specific vector components, the same names (i.e.,update,
internal , border
and external ) are sometimes used below to describe the vector
elements themselves. Having generalized these labels, the three types of
vector elements are distinguished by locally storing the internal
components first, followed by the border components and finally
by theexternal components. In addition, all external components
received from the same processor are stored consecutively. Below we summarize
the nomenclature for a processor with N total elements where N_internal
, N_border , and N_external elements are distributed over
the sets internal , border and external respectively.
| set | description | local numbering |
| internal | updated w/o communication | 0 to N_internal - 1 |
| border | updated with communication | N_internal to N_internal+ N_border-1. |
| external | not updated but used to update border | N_internal + N_border to N -1. elements received from the same processor are numbered consecutively. |
Similar to vectors, a subset of matrix non-zeros is stored on each processor.
In particular, each processor stores only those rows which correspond to
its update set. For example, if vector element i is updated
on processor p, then processor p also stores all the non-zeros
of row i in the matrix. Further, the local numbering of vector elements
on a specific processor induces a local numbering of matrix rows and columns.
For example, if vector element k is locally numbered as kl,
then all references to row k or column k in the matrix would
be locally numbered as kl. Thus, each processor contains a submatrix
whose row and column entries correspond to variables defined on this processor.
The remainder of this section describes the two sparse matrix for mats
that are used to store the local renumbered submatrix. These two sparse
matrix formats correspond to common formats used in serial computations.
3.1.
Distributed Modified Sparse Row (DMSR) Format. The DMSR for mat
is a generalization of the MSR format [3]. The data structure consists
of an integer vector bindx and a double precision vector val
each of length N_nonzeros + 1 where N_nonzeros is the number
of nonzeros in the local submatrix. For a submatrix with m rows
the DMSR arrays are as follows:
bindx:
| bindx(0) | m+1 |
| bindx[k+1]-bindx[k] | =number of nonzero off-diagonal elements in k'th row,k < m |
| bindx[ks,...ke] | =column indices of the off-diagonal nonzeros in row k where ks=bindx[k] and ke=bindx[k+1]-1. |
val:
| val[k] | =A[k,k], k< m |
| val[ki] | =the(k,bindx[ki])'th matrix element where |
Note: val[m] is not used. See [1] for a detailed discussion of the
MSR format.
3.2.
Distributed Variable Block Row (DVBR) Format. The Distributed
Variable Block Row (DVBR) format is a generalization of the VBR format
[1]. The
data structure consists of a double precision vector val and five integer
vectors:
indx , bindx , rpntr , cpntr ,bpntr . The format is best suited
for sparse
block matrices of the form
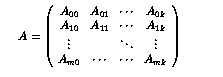
where Aij denotes a block (or submatrix). In a sparse block matrix,
some of these blocks would be entirely zero while others may be dense.
The DVBR vectors are described below for a matrix with M * K blocks.
rpntr[0 ... M] :
| rpntr[0] | = 0 |
| rpntr[k+1] -rpntr[k] | = number of rows in k 'th block row |
cpntr[0 ... K] :
| cpntr[0] | = 0 |
| cpntr[k+1] -cpntr[k] | = number of columns in k 'th block column |
bpntr[0 ... M] :
| bpntr[0] | = 0 |
| bpntr[k+1] - bpntr[k] | = number of nonzero blocks in the k 'th block row |
bindx[0 ... bpntr[M] ] :
| bindx[ks ... ke] | = block column indices of nonzero blocks in block row k where ks = bpntr[k] and ke = bpntr[k+1]-1 |
indx[0 ... bpntr[M] ] :
| indx[0] | = 0 |
| indx[ki+1] - indx[ki] | = number of nonzeros in the (k, bindx[ki] )'th block where |
val[0 ... indx[bpntr[M]] ] :
| val[is ... ie] | = nonzeros in the (k, bindx[ki] )'th block stored in column major order where ki is as defined above, is = indx[ki] and ie = indx[ki+1]-1 |
See [1] for a detailed discussion of the VBR format.
contents
4. High Level Data Interface.Setting
up the distributed format described in Section 3 for the local submatrix
on each processor can be quite cumbersome. In particular, the user must
determine a mapping between the global numbering scheme and a local scheme
which facilitates proper communication. Further, a number of additional
variables must be set for communication and synchronization (see Section
6).
In this section we describe a simpler data format that is used in conjunction
with a transformation function to generate data structures suitable for
Aztec. The new format allows the user to specify the rows in a natural
order as well as to use global column numbers in the bindx array.
To use the transformation function the user supplies the update
set and the submatrix for each processor. Unlike the previous section,
however, the submatrix is specified using the global coordinate numbering
instead of the local numbering required by Aztec.This procedure
greatly facilitates matrix specification and is the main advantage of the
transformation software.
On a given processor, the update set (i.e. vector element assignment
to processors) is defined by initializing the array update on each
processor so that it contains the global index of each element assigned
to the processor. The update array must be sorted in ascending order
(i.e. i < j => update[i] < update[j]). This sorting
can be performed using the Aztec function AZ_sort. Matrix specification
occurs using the arrays defined in the previous section. However, now the
local rows are defined in the same order as the update array and
column indices (e.g. bindx) are given as global column indices.
To illustrate this in more detail, consider the following example matrix:
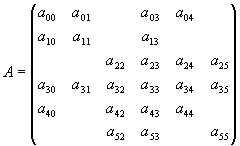
Figure 4 illustrates the information corresponding
to a particular matrix partitioning that is specified by the user as input
to the data transformation tool. Using this information, AZ_transform
A sample transformation is given in Figure 5 and is found in the file
az_app_utils_c. AZ_read_update is an Aztec utility which reads a
file and assigns elements to update. The user supplied routine create_matrix
creates an MSR or VBR matrix using the global numbering. Once transformed
the matrix can now be used within Aztec.
contents
5. Examples. A sample program is described
by completing the program fragments given earlier (Figures 1, 2 and 5).
In Figure 1, AZ_processor_info is an Aztec
utility which initializes the array proc_config to reflect the number
of processors being used and the node number of this processor. The function
AZ_solve is also supplied by Aztec to solve the user supplied linear
system. Thus, the only functions that the user must supply which have not
already been discussed include: init_guess_and_rhs in Figure
1 and create_matrix in Figure 5.
The function init_guess_and_rhs initializes the initial guess and the
right hand side. In Figure 6, a sample routine is
given which sets the initial guess vector to zero and sets the right hand
side vector equal to the global indices (where the local element update_index[i]
corresponds to global element update[i] , see Section 4)(
Alternatively, i could replace update_index[i] by invoking
AZ_reorder_vec() once rhs was initialized.).
A create_matrix function to initialize an MSR matrix is illustrated in
Figure 7. Different matrix problems can be implemented
by changing the function add_row which computes the MSR entries corresponding
to a new row of the matrix. The specific add_row function for implementing
a 5-point 2D Poisson operator on an n * n grid is shown in Figure
8 (n is a global variable set by the user). With these few lines
of code and the functions described earlier, the user initializes and solves
a 2D Poisson prob lem. While for simplicity of presentation this specific
example is structured the Aztec library does not assume any structure
in the sparse matrix. All the communication and variable renumbering is
done automatically without the assumption of structured communication.
Other add_row functions corresponding to a 3D Poisson equation and a high
order 2D Poisson equation are distributed with Aztec (file az_examples.c).
We recommend that potential users review at these examples. In many cases,
new applications can be written by simply editing these programs. The interested
reader should note that only a few lines of code are different between
the functions for the 5-pt Poisson, the high order Poisson and the 3D Poisson
codes. Further, the add_row routines are essentially identical to those
that would be used to set up sparse matrices in serial applications and
that there are no references to processors, communications or anything
specific to parallel programming.
Examples_____________________________________________________
proc 0:
N_update: 3
update: 0 1 3
bindx: 4 7 9 14 1 3 4 0 3 0 1
2 4 5
val: a00 a11 a33 - a01 a03 a04 a10 a13 a30 a31 a32 a34 a35
-----------------------------------------------------------------------
proc 1:
N_update: 1
update: 4
bindx: 2 5 0 2 3
val: a44 - a40 a42 a43
-----------------------------------------------------------------------
proc 2:
N_update: 2
update: 2 5
bindx: 3 6 8 3 4 5 2 3
val: a22 a55 - a23 a24 a25 a52 a53
Fig. 4. User input (MSR format) to initialize the sample matrix problem.
Example_______________________________________________________
init_matrix_vector_structures(bindx, val, update, external,
update_index, extern_index, data_org);
{
AZ_read_update(update, N_update);
create_matrix(bindx, val, update, N.update);
AZ_transform(bindx, val, update, external, update_index,
extern_index, data_org, N_update);
}
Fig. 5. init_matrix_vector_structures.
Example_________________________________________________
void init_guess_and_rhs(x, rhs, data_org, update, update_index)
{
N_update = data_org[AZ_N_internal] + data_org[AZ_N_border];
for (i = 0; i < N_update ; i = i + 1) {
rhs[update_index[i]] = (double) update[i];
x[i] = 0.0;
}
}
Fig. 6. init_guess_and_rhs.
Example________________________________________________
void create_matrix(bindx, val, update, N_update)
{
N_nonzeros = N_update + 1;
bindx[0] = N_nonzeros;
for (i = 0; i < N_update; i = i + 1)
add_row(update[i], i, val, bindx);
}
Fig. 7. create_matrix.
Example_____________________________________________________
void add_row(row, location, val, bindx)
{
k = bindx[location]; val[location] = 4.; /* matrix diagonal */
/* check neighboring points in each direction and add nonzero */
/* entry if neighbor exists. */
bindx[k] = row + 1; if (row%n != n-1) val[k++] = -1.;
bindx[k] = row - 1; if (row%n != 0) val[k++] = -1.;
bindx[k] = row + n; if ((row/n)%n != n-1) val[k++] = -1.;
bindx[k] = row - n; if ((row/n)%n != 0) val[k++] = -1.;
bindx[location+1] = k;
}
Fig. 8. add_row for a 2D Poisson problem
Example _______________________________________________
void create_matrix(bindx, val, update, N_update);
{
read_triangles(T, N_triangles);
init_msr(val, bindx, N_update);
for (triangle = 0; triangle < N_triangles; triangle = triangle + 1)
for (i = 0; i < 3; i = i + 1) {
row = AZ_find_index(T[triangle][i], update,N_update);
for (j = 0; j <3; j = j + 1) {
if (row != NOT_FOUND)
add_to_element(row, T[triangle][j], 0.0, val, bindx, i==j);
}}}
compress_matrix(val, bindx, N_update);
}
Fig. 9. create_matrix for the Poisson finite element problem.
While Aztec simplifies the parallel coding associated with structured
problems, it is for unstructured problems that Aztec makes a significant
programming difference. To illustrate this, a 2D finite element example
is given where the underlying grid is a triangulation of a complex geometry.
Unlike the previous example create_matrix de fines a sparsity pattern (i.e.
bindx ) but not the actual nonzero entries (i.e. val ) as
interprocessor communication is required before they can be computed. Thus,
in this example AZ_transform takes the sparsity pattern and initializes
the communication data structures. Using these structures, communication
can be performed at a later stage in computing the matrix nonzeros.
Figure 9 depicts create_matrix while Figure
10 depicts an additional function matrix_fill that must be included
before AZ_solve is invoked in Figure 1. We have not made any effort to
optimize these routines. In both figures the new lines that have been added
specifically for a parallel implementation are underlined. That is, create_matrix
and matrix_fill have been created by taking a serial program that creates
the finite element discretization, splitting this program over the two
functions and adding a few new lines necessary for the parallel implementation.
The only additional change is to replace the single data file containing
the triangle connectivity read using read_triangles by a set of data files
containing the triangle connectivity for each processor. We do not discuss
the details of this program but only wish to draw the readers attention
to the small number of lines that need changing to convert the serial unstructured
application to parallel. Most of the main routines such as setup_Ke which
computes the element contributions and add_to_element which stores the
element contributions in the MSR data structures remain the same. In fact,
almost all the new lines of code correspon to adding the communication
(AZ_exchange_bdry) (which was the main reason that the calculation of the
matrix nonzeros was deferred) and the conversion of global index values
by local index values with the help of AZ_find_index. As in the Poisson
example, all of the details with respect to communication are hidden from
the user.
Example_____________________________________
void matrix_fill(bindx, val, N_update, update, update_index,
N_external, external, extern_index)
/* read the x and y coordinates from an input file */
for (i = 0; i < N_update; i = i + 1){
read_from_file(x[update_index[i]], y[update_index[i]]);
}
AZ_exchange_bdry(x);
AZ_exchange_bdry(y);
/* Locally renumber the rows and columns of the new sparse matrix */
for (triangle = 0; triangle < N_triangles; triangle = triangle + 1)
for (i = 0; i < 3; i = i + 1) {
row = AZ_find_index(T[triangle][i], update, N_update);
if (row == NOT_FOUND) {
row = AZ_find_index(T[triangle][i], external, N_external);
T[triangle][i] = extern_index[row];
}
else T[triangle][i] = update_index[row];
}
}
/* Fill the element stiffness matrix Ke */
for (triangle = 0; triangle < N_triangles; triangle = triangle + 1){
setup_Ke(Ke, x[T[triangle][0]], y[T[triangle][0]],
x[T[triangle][1]], y[T[triangle][1]],
x[T[triangle][2]], y[T[triangle][2]]);
/* Fill the sparse matrix by scattering Ke to appropriate locations */
for (i = 0; i < 3; i = i + 1) {
for (j = 0; j < 3; j = j + 1){
if (T[triangle][i] < N_update){
add_to_element(T[triangle][i], T[triangle][j], Ke[i][j],
val, bindx, i==j);
}
}
}
}
Fig. 10. matrix_fill for the Poisson finite element problem.
contents
6. Advanced Topics.
6.1. Data Layout. The Aztec
function AZ_transform initializes the integer array data_org. This
array specifies how the matrix is set up on the parallel machine. In many
cases, the user need not be concerned with the contents of this array.
However, in some
situations it is useful to initialize these elements without the use of
AZ_transform, to
access these array elements (e.g. determine how many internal components
are used), or to change these array elements (e.g. when reusing factorization
information, see Section 6.2). When using the transformation software,
the user can ignore the size of data_org as it is allocated in AZ_transform.
However, when this is not used, data_org must be allocated of size
AZ_COMM_SIZE + number of vector elements sent to other processors during
matrix-vector multiplies. The contents of data_org are as follows:
Specifications_________________________________________
| data_org[AZ_matrix_type] | Specifies matrix format. |
| AZ_VBR_MATRIX | Matrix corresponds to VBR format. |
| AZ_MSR_MATRIX | Matrix corresponds to MSR format. |
| data_org[AZ_N_internal] | Number of elements updated by this processor that can be computed without information from neighboring processors (N_internal ). This also corresponds to the number of internal rows assigned to this processor. |
| data_org[AZ_N_border] | Number of elements updated by this processor that use information from neighboring processors (N_border ). |
| data_org[AZ_N_external] | Number of external components needed by this processor (N_external ). |
| data_org[AZ_N_int_blk] | Number of internal VBR block rows owned by this processor. Set to data_org[AZ_N_internal] for MSR matrices. |
| data_org[AZ_N_bord_blk] | Number of border VBR block rows owned by this processor. Set to data_org[AZ_N_border] for MSR matrices. |
| data_org[AZ_N_ext_blk] | Number of external VBR block rows on this processor. Set to data_org[AZ_N_external] for MSR matrices. |
| data_org[AZ_N_neigh] | Number of processors with which we exchange infor mation (send or receive) in performing matrix-vector products. |
| data_org[AZ_total_send] | Total number of vector elements sent to other processors during matrix-vector products. |
| data_org[AZ_name] | Name of the matrix. This name is utilized when decid ing which previous factorization to use as a preconditioner (see Section 6.2). (positive integer value). |
| data_org[AZ_neighbors] | Start of vector containing node i.d.'s of neighboring processors. That is, data_org[AZ_neighbors+i] gives the node i.d. of the (i+1 )'th neighbor. |
| data_org[AZ_rec_length] | Start of vector containing the number of elements to receive from each neighbor. We receive from the (i+1 )'th neighbor data_org[AZ_rec_length+i] elements. |
| data_org[AZ_send_length] | Start of vector containing the number of elements to send to each neighbor. We send to the (i+1 )'th neighbor data_org[AZ_rec_length+i] elements. |
| data_org[AZ_send_list] | Start of vector indicating the elements that we will send to other processors during communication. The first data_org[AZ_send_length] components correspond to the elements for the first neighbor and the next data_org[AZ_send_length+1] components correspond to element indices for the second neighbor, and so on. |
6.2. Reusing factorizations.
When solving a problem, Aztec may create cer tain information that
can be reused later. In most cases, this information corresponds to either
matrix scaling factors or preconditioning factorization information for
LU or ILU. This information is saved internally and referenced by the matrix
name given by data_org[AZ_name]. By changing options[AZ_pre_calc]
and data_org[AZ_name] a number of different Aztec possibilities
can be realized. As an example, consider the following situation. A user
needs to solve the linear systems in the order shown below:
![]()
The first and second systems are solved with options[AZ_pre_calc]
set to AZ_calc. How ever, the name (i.e. data_org[AZ_name]) is changed
between these two solves. In this way, scaling and preconditioning information
computed from the first solve is not over written during the second solve.
By then setting options[AZ_pre_calc] to AZ_reuse and data_org[AZ_name]
to the name used during the first solve, the third system is solved reusing
the scaling information (to scale the right hand side, initial guess, and
rescale the final solution( The matrix does not need to be
rescaled as the scaling during the first solve overwrites the original
matrix.) and the preconditioning factorizations (e.g. ILU) used
during the first solve. While in this example the same matrix system is
solved for the first and third solve, this is not necessary. In particular,
preconditioners can be reused from previous nonlinear iterates even though
the linear system being solved are changing. Of course, many times information
from previous linear solves is not reused. In this case the user must explicitly
free the space associated with the matrix or this information will remain
allocated for the duration of the program. Space is cleared by invoking
AZ_free_memory(data_org[AZ_name]).
6.3. Important Constants.
Aztec uses a number of constants which are defined in the file az_aztec_defs.h.
Most users can ignore these constants. However, there may be situations
where they should be changed. Below is a list of these constants with a
brief description:
| AZ_MAX_NEIGHBORS | Maximum number of processors with which in formation can be exchanged during matrix-vector products. |
| AZ_MSG_TYPE AZ_NUM_MSGS | All message types used inside Aztec lie be tween AZ_MSG_TYPE and AZ_MSG_TYPE + AZ_NUM_MSGS - 1. |
| AZ_MAX_BUFFER_SIZE | Maximum message information that can be sent by any processor at any given time before receiv ing. This is used to subdivide large messages to avoid buffer overflows. |
| AZ_MAX_MEMORY_SIZE | Maximum available memory. Used primarily for the LU-factorizations where a large amount of memory is first allocated and then unused portions are freed after factorization. |
| AZ_TEST_ELE | Internal algorithm parameter that can effect the speed of the AZ_find_procs_for_externs calculation. Reduce AZ_TEST_ELE if communication buffers are exceeded during this calculation. |
6.4. AZ_transform Subtasks.
The function AZ_transform described in Section 4 is actually made up of
5 subtasks. In most cases the user need not be concerned with the individual
tasks. However, there might arise situations where additional information
is available such that some of the subtasks can be omitted. In this case,
it is possible forthe user to edit the code for AZ_transform located in
the file az_tools.c to suit the application. In this section we briefly
describe the five subroutines which make up the transformation function.
More detailed descriptions are given in [5]. Prototypes for these subroutines
as well as for AZ_transform are given in Section 7.
- AZ_transform begins by identifying the external set needed by
each processor. Here, each column entry must correspond to either an element
updated by this processor or an external component. The function - AZ_find_local_indices
checks each column entry. If a column is in update, its number is
replaced by the appropriate index into update (i.e. update[new
column index] = old column index). If a column number is not found
in update, it is stored in the external list and the column
number is replaced by an index into external (i.e. external[new
column index - N_update] = old column index).
- AZ_find_procs_for_externs queries the other processors to determine which
processors update each of its external components. The array
extern_proc is set such that extern_proc[i] indicates which
processor updates external[i] .
- AZ_order_ele reorders the external components such that elements
updated by the same processor are contiguous. This new ordering is given
byextern_index where extern_index[i] indicates the local
numbering of external[i] . Additionally, update components
are reordered so the internal components precede the border components.
This new ordering is given by update_index where update_index[i]
indicates the local num bering of update[i] .
- AZ_set_message_info initializes data_org (see Section 6.1)
This is done by computing the number of neighbors, making a list of the
neighbors, computing the number of values to be sent and received with
each neighbor and computing the list of elements which will be sent to
other processors during communication steps.
- Finally, AZ_reorder_matrix permutes and reorders the matrix nonzeros
so that its entries correspond to the newly reordered vector elements.
7. Aztec Functions . In this section we
describe the Aztec functions available to the user. Certain variables
appear many times in the parameter lists of these frequently used functions.
In the interest of brevity we describe these variables at the beginning
of this section and then proceed with the individual function descriptions.
Frequently Used Aztec Parameters___________________________
| data_org | Array describing the matrix format (Section 6.1). Allocated and set AZ_set_message_info and AZ_transform. |
| extern_index | extern_index[i] gives the local numbering of global element external[i] . Allocated and set by AZ_order_ele and AZ_transform. |
| extern_proc | extern_proc[i] is updating processor of external[i] . Allocated and set by AZ_find_procs_for_externs. |
| external | Sorted list (global indices) of external elements on this node. Allocated and set by AZ_find_local_indices and AZ_transform . |
| N_external | Number of external components. Set by AZ_find_procs_for_externs and AZ_transform. |
| N_update | Number of update components assigned to this proces sor. Set by AZ_read_update. |
| options, params | Arrays describing AZ_solve options (Section 2). |
| proc_config[AZ_node] | Node i.d. of this processor. |
| proc_config[AZ_N_procs] | Total number of processors used in current simulation. Allocated and set by AZ_processor_info. |
| update_index | update_index[i] gives the local numbering of global ele ment update[i] . Allocated and set by AZ_order_ele and AZ_transform. |
| update | Sorted list of elements (global indices) to be updated on this processor. Allocated and set by AZ_read_update. |
| val, bindx, bpntr, cpntr, indx, rpntr | Arrays used to store matrix. For MSR matrices bpntr, cpntr, indx, rpntr are ignored (Section 3). |
Prototype_________________________________________
void AZ_broadcast(char *ptr , int length, int *proc_config,
int action)
Description___________________________________________
Used to concatenate a buffer of information and to broadcast this information
from processor 0 to the other processors. The four possible actions are
* action == AZ_PACK
| - proc_config[AZ_node] == | 0: store ptr in the internal buffer. |
| - proc config[AZ_node] not= | 0: read from the internal buffer to ptr . If the internal buffer is empty, first receive the broadcast information. |
* action == AZ_SEND
| - proc_config[AZ_node] == | 0: broadcast the internal buffer (filled by AZ_broadcast) and then clear it. |
| - proc_config[AZ_node] not= | 0: clear internal buffer. |
Sample Usage:
The following code fragment broadcasts the information in `a' and `b'.
if (proc_config[AZ_node] == 0) {
a = 1;
b = 2;
}
AZ_broadcast(&a, sizeof(int), proc_config, AZ_PACK);
AZ_broadcast(&b, sizeof(int), proc_config, AZ_PACK);
AZ_broadcast(NULL , 0 , proc_config, AZ_SEND);
NOTE: There can be no other communication calls between the AZ_PACK
and AZ_SEND calls to AZ_broadcast.
Parameters_________________________________________________________
| ptr | On input, data string of size length. Information is either stored to or retrieved from ptr as described above. |
| length | On input, length of ptr to be broadcast/received. |
| action | On input, determines AZ_broadcast behavior. |
Prototype_____________________________________________________________
int AZ_check_input(int *data_org, int *options, double *params,
int *proc_config)
Description___________________________________________________________
Perform checks for iterative solver library. This is to be called by the
user of the solver library to check the values in data_org; options;
params; and proc_config. If all the values are valid AZ_check_input
returns 0, otherwise it returns an error code which can be deciphered using
AZ_print_error.
Aztec Functions
Prototype____________________________________________________________
void AZ_check_msr(int *bindx , int N_update, int N_external
, int option, int *proc_config)
Description_____________________________________________________________
Check that the number of nonzero off-diagonals in each row and that the
column indices are nonnegative and not too large (see option).
Parameters_____________________________________________________________
option
| AZ_LOCAL | On input, indicates matrix uses local indices. The number of nonzeros in a row and the largest column index must not exceed the total number of elements on this processor. |
| AZ_GLOBAL | On input, indicates matrix uses global indices. The number of nonzeros in a row and the largest column index must not exceed the total number of elements in the simulation. |
Aztec Functions
Prototype___________________________________________________________
void AZ_check_vbr(int N_update, int N_external , int option,
int *bindx , int *bpntr , int *cpntr , int *rpntr
, int *proc_config )
Description_________________________________________________________
Check VBR matrix for the following:
* number of columns within each block column is nonnegative.
* rpntr[i] == cpntr[i] for i =< N_update.
* number of nonzero blocks in each block row is nonnegative and not too
large.
* block column indices are nonnegative and not too large.
Parameters_________________________________________________________
option
| AZ_LOCAL | On input, indicates matrix uses local indices. The number of block nonzeros in a row and the largest block column index must not exceed the total number of blocks columns on this processor. |
| AZ_GLOBAL | On input, indicates matrix uses global indices. The number of block nonzeros in a row and the largest block column index must not exceed the total number of blocks rows in the simulation. |
Aztec Functions
Prototype__________________________________________________________
int AZ_defaults(int *options, double *params )
Description_______________________________________________
Set options and params so that the default options are chosen.
Parameters_______________________________________________
| options | On output, set to the default options. |
| params | On output, set to the default parameters. |
Aztec Functions
Prototype_____________________________________________
void AZ_exchange_bdry(double *x , int *data_org)
Description______________________________________________
Locally exchange the components of the vector x so that the external
components of x are updated.
Parameters____________________________________________
| x | On input, vector defined on this processor. On output, external components of x are updated via communication. |
Aztec Functions
Prototype____________________________________________
int AZ_find_index(int key, int *list , int length
)
Description__________________________________________
Returns the index, i, in list (assumed to be sorted) which
matches the key (i.e. list[i] == key). If key is not found
AZ_find_index returns -1. See also AZ_quick_find.
Parameters_______________________________________________
| key | On input, element to be search for in list. |
| list | On input, sorted list to be searched. |
| length | On input, length of list. |
Aztec Functions
Prototype_______________________________________________
| void AZ_find_local_indices( | int N_update, int *bindx , int *update, int **external , int *N_external , int mat_type, int *bpntr ) |
Description_______________________________________________
Given the global column indices for a matrix and a list of elements updated
on this processor, compute the external set and change the global
column indices to local column indices. Specifically,
* allocate external , compute and store the external components
in external .
* renumber column indices so that column entry k is renumbered as
j where either update[j] == k or external[j-N_update]
== k .
Called by AZ_transform.
Parameters_________________________________________________
| mat_type | On input, indicates whether matrix format is MSR (= AZ_MSR_MATRIX) or VBR (= AZ_VBR_MATRIX). |
| external | On output, allocated and set to sorted list of the external elements. |
| bindx | On input, contains global column numbers of MSR or VBR matrix (Section 3). On output, contains local column numbers as described above. |
Aztec Functions
Prototype_________________________________________________
void AZ_find_procs_for_externs(int N_update, int *update,
int *external , int N_external , int *proc_config,
int **extern_proc)
Description __________________________________________________
Determine which processors are responsible for updating each external element.
Called by AZ_transform.
Parameters___________________________________________________
| extern_proc | On output, extern_proc[i] contains the node number of the processor which updates external[i]. |
Aztec Functions
Prototype___________________________________________________
void AZ_free_memory(int name)
Description_________________________________________________
Free Aztec memory associated with matrices with data_org[AZ_name]
= name. This is primarily scaling and preconditioning information
that has been computed on
earlier calls to AZ_solve.
Parameters__________________________________________________
| name | On output, all preconditioning and scaling information is freed for matrices which have data_org[AZ name] =name |
Prototype___________________________________________________
double AZ_gavg_double(double value, int *proc_config )
Description _________________________________________________
Return the average of the numbers in value on all processors.
Parameters___________________________________________________
| value | On input, value contains a double precision number. |
Aztec Functions
Prototype______________________________________________________
double AZ_gdot(int N , double *r , double *z , int
*proc_config )
Description_________________________________________________
Return the dot product of r and z with unit stride. This
routine calls the BLAS routine ddot to do the local vector dot product
and then uses the global summation
routine AZ_gsum_double to obtain the required global result.
Parameters__________________________________________________
| N | On input, length of r and z on this processor. |
| r, z | On input, vectors distributed over all the processors. |
Aztec Functions
Prototype_____________________________________________________
double AZ_gmax_double(double value, int *proc_config )
Description _______________________________________________
Return the maximum of the numbers in value on all processors.
Parameters________________________________________________
| value | On input, value contains a double precision number. |
Aztec Functions
Prototype__________________________________________________
int AZ_gmax_int(int value, int *proc_config )
Description _______________________________________________
Return the maximum of the numbers in value on all processors.
Parameters_________________________________________________
| value | On input, value contains an integer. |
Aztec Functions
Prototype_________________________________________________
| double AZ_gmax_matrix_norm( | double *val , int *indx , int *bindx , int *rpntr , int *cpntr , int *bpntr , int *proc_config, int *data_org) |
Description_______________________________________________
Returns the maximum matrix norm ![]() for the distributed matrix encoded in val, indx, bindx, rpntr, cpntr,
bpntr (Section 3).
for the distributed matrix encoded in val, indx, bindx, rpntr, cpntr,
bpntr (Section 3).
Aztec Functions
Prototype_________________________________________________
double AZ_gmax_vec(int N , double *vec, int *proc_config
)
Description_________________________________________
Return the maximum of all the numbers located in vec[i] (i < N )
on all processors.
Parameters_____________________________________________
| vec | On input, vec contains a list of numbers. |
| N | On input, length of vec. |
Aztec Functions
Prototype_____________________________________________
double AZ_gmin_double(double value, int *proc_config )
Description_____________________________________________
Return the minimum of the numbers in value on all processors.
Parameters_________________________________________________
| value | On input, value contains a double precision number. |
Aztec Functions
Prototype_________________________________________________
int AZ_gmin_int(int value, int *proc_config )
Description_________________________________________________
Return the minimum of the numbers in value on all processors.
Parameters__________________________________________________
value On input, value contains an integer.
Aztec Functions
Prototype_____________________________________________________
double AZ_gsum_double(double value, int *proc_config )
Description___________________________________________________
Return the sum of the numbers in value on all processors.
Parameters____________________________________________________
value On input, value contains a double precision number.
Aztec Functions
Prototype______________________________________________________
int AZ_gsum_int(int value, int *proc_config )
Description_____________________________________________________
Return the sum of the integers in value on all processors.
Parameters_______________________________________________________
value On input, value contains an integer.
Aztec Functions
Prototype____________________________________________________
void AZ_gsum_vec_int(int *values, int *wkspace, int length,
int *proc_config )
Description__________________________________________________
values[i] is set to the sum of the input numbers in values[i]
on all processors (i < length).
Parameters__________________________________________________
| values | On input, values contains a list of integers. On output, values[i] contains the sum of the input values[i] on all the processors. |
| wkspace | On input, workspace array of size length. |
| length | On input,length of values and wkspace. |
Aztec Functions
Prototype____________________________________________________
double AZ_gvector_norm(int n, int p, double *x , int
*proc_config)
Description____________________________________________________
Returns the p norm of the vector x distributed over the processors:
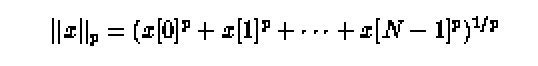
where N is the total number of elements in x over all processors.
NOTE: For the ![]() norm, set p
= - 1.
norm, set p
= - 1.
Parameters_____________________________________________________
| n | On input, number of update components of x on this processor. |
| p | On input, order of the norm to perform, i.e., |
| x | On input, vector whose norm will be computed. |
Aztec Functions
Prototype___________________________________________________
void AZ_init_quick_find(int *list , int length, int *shift
, int *bins )
Description___________________________________________________
shift and bins are set so that they can be used with AZ_quick_find.
On output, shift satisfies
![]() and
and ![]()
where range = list[length - 1] - list[0] . The array bins
must be of size 2 + length/4 and is set so that
![]()
where ![]() .
.
This routine is used in conjunction with AZ_quick_find. The idea is to
use bins to get a good initial guess as to the location of value
in list .
Parameters_______________________________________________________
| list | On input, sorted list . |
| length | On input, length of list . |
| shift | On output, shift is set as described in above. |
| bins | On input, array of size 2 + length/4. On output, bins is set as described above. |
Aztec Functions
Prototype________________________________________________________
void AZ_invorder_vec(double *x , int *data_org, int *update_index
, int *rpntr , double *untrans_x )
Description______________________________________________________
Untransform the vector x whose data layout corresponds to a transformed
matrix (see AZ_transform or AZ._reorder_matrix) so that the new vector
(untrans_x) corresponds to data in the original user-given ordering.
Parameters_________________________________________
| x | On input, distributed vector whose data layout corresponds to a transformed matrix. |
| untrans_x | On output, the result of untransforming x so that the data-layout
now corresponds to the original ordering given by the user. |
Prototype_____________________________________
| void AZ_matvec_mult | (double *val , int *indx , int *bindx , int *rpntr , int *cpntr , int *bpntr , double *b, double *c, int exchange_flag, int *data_org ) |
Description_____________________________________
Perform the matrix-vector multiply
![]()
where the matrix A is encoded in val, indx, bindx, rpntr, cpntr, bpntr
(Section 3).
Parameters_____________________________________________
| b | On input, distributed vector to use in multiplication. NOTE: b should contain data_org[AZ_N_internal] + data_org[AZ_N_border] + data_org[AZ_N_external] elements (though external variables stored at the end of the vector do not need to be initialized). |
| c | On output, the result of matrix-vector multiplication. NOTE: c should contain data_org[AZ_N_internal] + data_org[AZ_N_border] elements. |
| exchange_flag | On input, dictates whether communication needs to oc cur. If exchange_flag == 1, communication occurs. If exchange_flag == 0, no communication occurs. |
Aztec Functions
Prototype_____________________________________________________
| void AZ_msr2vbr( | double *val , int *indx , int *rpntr , int *cpntr , int *bpntr , int *bindx , int *bindx2 , double *val2 , int total_blk_rows, int total_blk_cols, int blk_space ,int nz_space, int blk_type) |
Description______________________________________
Convert the DMSR matrix defined in (val2; bindx2) to a DVBR matrix
defined in (val, indx, rpntr, cpntr, bpntr, bindx).
Parameters_______________________________________
| val2, bindx2 | On input, DMSR arrays holding the matrix to be converted. |
| cpntr | On input, cpntr[i] is the block size of the i^th block in the resulting DVBR matrix. Columns 0 to cpntr[0] - 1 form the first block column, columns cpntr[0] to cpntr[0] + cpntr[1] - 1 form the second block column, etc. On output, cpntr corresponds to the resulting DVBR matrix. |
| val, indx, rpntr, bpntr, bindx |
On output, DVBR arrays of converted DMSR matrix. |
| total_blk_rows | On input, number of block rows in resulting local VBR matrix. |
| total_blk_cols | On input, number of block columns in resulting local VBR matrix. |
| blk_space | On input, length allocated for bindx and indx. |
| nz_space | On input, length allocated for val. |
| blk_type | On input, if blk_type > 0, indicates that all block rows (and columns) have the same size given by blk_type. If blk_type < 0 , the block rows have different sizes. |
Aztec Functions
Prototype____________________________________________________
| void AZ_order_ele( | int *update_index , int *extern_index , int *N_internal , int *N_border , int N_update, int *bpntr , int *bindx , int *extern_proc, int N_external , int option, int mat_type) |
Description_______________________________________
Find orderings for update and external . external are ordered
so that elements updated by the same processor are contiguous. If option
== AZ_ALL, update are ordered so that the internal components
have the lowest numbers followed by the border components. Otherwise,
the order of update is unchanged. The ordering information is placed
in update_index and extern_index (Section 4). Called by AZ_transform.
Parameters_________________________________________
| N_internal | On output, number of internal components on processor. |
| N_border | On output, number of border components on processor. |
| update_index | On output, update_index[i] indicates the local index (or order) of update[i]. |
| extern_index | On output, extern_index[i] indicates the new local index (or order) of external[i]. |
| option | On input, indicates whether to reorder update. |
| AZ_ALL | Order update and external. |
| AZ_EXTERNS | Order only external elements. |
| mat_type | On input, indicates whether matrix format is MSR (= AZ_MSR_MATRIX) or VBR (= AZ_VBR_MATRIX). |
Prototype_____________________________________________
void AZ_print_error(int error_code)
Description ___________________________________________
Prints out an error message corresponding to error_code. Typically,
error_code is generated by AZ_check_input.
Parameters_____________________________________________________
error_code On input, error code generated by AZ_check_input.
Aztec Functions
Prototype_________________________________________________________
| void AZ_print_out( | int *update_index, int *extern_index, int *update, int *external, double *val, int *indx, int *bindx, int *rpntr, int *cpntr, int *bpntr, int *proc_config, int choice, int matrix_type, int N_update, int N_external, int offset ) |
Description_______________________________________________________
Print Aztec matrices in one of several formats:
| choice | On input, selects output format as described above. |
| matrix_type | On input, matrix format: either AZ_VBR_MATRIX or AZ_MSR_MATRIX. |
| N_update | On input, number of (block) rows assigned to processor. |
| N_external | On input, data_org[AZ_N_ext_blks]. |
| offset | On input, row and column offset. See above description. |
Aztec Functions
Prototype__________________________________________________________________
void AZ_processor_info(int *proc_config)
Description________________________________________________________________
proc_config[AZ_node] is set to the node name of this processor.
proc_config[AZ_N_proc] is set to the number of processors used in
simulation.
Aztec Functions
Prototype_________________________________________________________________
int AZ_quick_find(int key, int *list , int length,
int shift , int *bins )
Description__________________________________________________________________
Return the index, i, in list (assumed to be sorted) which
matches the key (i.e. list[i] = key). If key is not found
AZ_quick_find returns -1.
NOTE: This version is faster than AZ_find_index but requires bins
to be set and stored using AZ_init_quick_find.
Parameters________________________________________________________________
| key | On input, element to search for in list . |
| list | On input, sorted list to be searched. |
| length | On input, length of list. |
| shift | On input, used for initial guess (computed by previous AZ_init_quick_find call). |
| bins | On input, computed by AZ_init_quick_find for initial guess. bins is set so that list[bins[k]] <= key < list[bins[k + 1]] where k = (key - list[0])/2^shift . |
Aztec Functions
Prototype_________________________________________________________________
| void AZ_read_msr_matrix( | int *update, double **val , int **bindx , int
N_update, int *proc_config ) |
Description__________________________________________________________________
Read the file .data and create a matrix in the MSR format. Processor 0
reads the input file. If the new row to be added resides in processor 0's
update, it is added to processor 0's matrix. Otherwise, processor 0
determines which processor has requested this row and sends it to this
processor for its local matrix.
The form of the input file is as follows:
| num_rows | |||
| col_num1 | entry1 | col_num2 | entry2 |
| col_num3 | entry3 | -1 | |
| col_num4 | entry4 | col.num5 | entry5 |
| col_num6 | entry6 | -1 |
This input corresponds to two rows: 0 and 1. Row 0 contains entry1 in column
col_num1, entry2 in column col_num2 and entry3 in column col_num3. Row
1 contains entry4 in column col_num4, entry5 in column col_num5 and entry6
in column col_num6. When using exponential notation, `E' or `e' should
be used instead of `D' or `d'. Additionally, it is important that row and
column numbers be labelled from 0 to n-1 and not 1 to n where n is the
number of rows.
NOTE: Spacing and carriage returns are not important.
NOTE: AZ_read_msr_matrix() is inefficient for large matrices. It is, however,
possible to read binary files. In particular, if Aztec is compiled
with a -Dbinary option, `.data' must contain binary integers and binary
double precision numbers in the same form as above except without spaces
or carriage returns between numbers. Since binary formats are not standard,
`.data' should be created using a `C' program via fread() and fwrite()
executed on the same machine as Aztec.
Parameters___________________________________________________________________
| val, bindx | On output, these two arrays are allocated and filled with the MSR representation corresponding to the file .data. |
Aztec Functions
Prototype_________________________________________________________
| void AZ_read_update( | int *N_update, int **update, int *proc_config, int N , int chunk , int input_option ) |
Description_____________________________________________
This routine initializes update to the global indices updated by
this processor and initializes N_update to the total number of elements
to be updated.
Parameters_______________________________________________________
| N_update | On output, number of elements updated by processor. |
| update | On output, update is allocated and contains a list of elements updated by this processor in ascending order. |
| chunk | Number of indices within a group. For example, chunk == 2 => chunk0 = {0, 1}, and chunk1 = {2, 3}. |
| N | Total number of chunks in the vector. |
| input_option | |
| AZ_linear | Processor 0 is assigned the first |
| AZ_box | The processor system is viewed as a p2 * p1 * p0 array while the matrix problem corresponds to a n2 * n1 * n0 grid with `chunks' unknowns at each grid point. The user is prompted for the pi's and the xi's. Assuming that the grid is ordered `naturally' or lexicographically, the grid is subdivided into uniform boxes whose corresponding rows are to be assigned to each processor. |
| AZ_file | Read the proc_config[AZ_N_proc] lists contained in the file .update. Each list contains a set of global indices preceeded by the of number of indices in this set. List 0 is sent to processor proc_config[AZ_N_proc] - 1, list 1 is sent to processor proc_config[AZ_N_proc] - 2, etc. Note: A graph partitioning package named Chaco [2] produces files in this format. |
Aztec Functions
Prototype______________________________________________________
| void AZ_reorder_matrix( | int N_update, int *bindx , double *val , int *update_index , int *extern_index , int *indx , int *rpntr , int *bpntr , int N_external , int *cpntr , int option, int mat_type) |
Description______________________________________________________
Reorder the matrix so that it corresponds to the new ordering given by
update_index and extern_index . Specifically, global matrix
entry (update[i], update[j]) which was stored as local matrix entry
(i, j) is stored as (update_index[i], update_index[j]) on output.
Likewise, global matrix entry (update[i], external[k]) which was
stored as local matrix entry (i, k + N_update) is stored locally
as (update_index[i], extern_index[k]) on output. Called by AZ_transform.
IMPORTANT: This routine assumes that update_index contains two sequences
of numbers that are ordered but intertwined. For example,
| update_index : | 4 5 0 6 1 2 3 7 |
| sequence 1: | 0 1 2 3 |
| sequence 2: | 4 5 6 7 |
See also AZ_reorder_vec and AZ_invorder_vec to tranform the right hand
side and solution vectors.
Parameters_____________________________________________________________
| option | On input, indicates whether to reorder update elements. |
| AZ_ALL | All the rows and columns are renumbered. |
| AZ_EXTERNS | Only columns corresponding to external elements are renumbered. |
| mat_type | On input, indicates matrix format. |
| AZ_MSR_MATRIX | DMSR matrix format. |
| AZ_VBR_MATRIX | DVBR matrix format. |
| bindx, val, indx, rpntr, bpntr, cpntr | On input, matrix ordered as described above. On output, matrix reordered using update_index and extern_index as described above. |
Prototype_____________________________________________________________
void AZ_reorder_vec(double *x , int *data_org, int *update_index
, int *rpntr )
Description___________________________________________________
Transform the vector x whose data layout corresponds to the user-given
ordering (i.e. x[i] corresponds to global vector element x[update[i]])
so that now the data corresponds to a transformed matrix (see AZ_transform
or AZ._reorder_matrix).
Parameters___________________________________________________
| x | On input, distributed vector whose data layout corre sponds to the original ordering given by the user. On output, the data layout now corresponds to a transformed matrix whose ordering is given by update_index . |
Aztec Functions
Prototype___________________________________________________
| void AZ_set_message_info( | int N_external , int *extern_index , int N_update, int *external , int *extern_proc, int *update, int *update_index , int *proc_config, int *cpntr , int ** data_org, int mat_type) |
Description___________________________________________
Initialize data_org so that local communications can occur to support
matrix vector products. This includes:
Called by AZ_transform.
NOTE: Implicitly the neighbors are numbered using the ordering of the external
elements (which have been previously ordered such that elements updated
by the same processor are contiguous).
Parameters___________________________________________
| data_org | On output, data_org is allocated and completely initialized as described in Section 6.1. |
| mat_type | On input, indicates matrix format. |
| AZ_MSR_MATRIX | DMSR matrix. |
| AZ_VBR_MATRIX | DVBR matrix. |
Aztec Functions
Prototype_____________________________________________
| void AZ_solve( | double *x , double *b, int *options, double *params, int *indx ,int *bindx , int *rpntr , int *cpntr , int *bpntr , double *val , int *data_org, double *status, int *proc_config) |
Description_______________________________________
Solve the system of equations Ax = b via an iterative method where
the matrix A is encoded in indx, bindx, rpntr, cpntr, bpntr
and val (see Section 3 and Section 2).
Parameters_________________________________________
| x | x is the initial guess on input and the linear system solution on output. NOTE: x should contain data_org[AZ_N_internal] + data_org[AZ_N_border] + data_org[AZ_N_external] elements (though external variables stored at the end of the vector do not need to be initialized). |
| b | A data_org[AZ_N_internal] + data_org[AZ_N_border] length vector containing the right hand side. |
| options,params | Options and parameters used during the solution process (Section 2). |
| status | On output, status of iterative solver (Section 2). |
Aztec Functions
Prototype__________________________________________
void AZ_sort(int *list1 , int N , int *list2 , double
*list3 )
Description_______________________________________
Sort the elements in list1 . Additionally, move the elements in
list2 and list3 so that they correspond with the moves done
to list . NOTE: If list2 == NULL, list2 is not manipulated.
If list3 == NULL, list3 is not manipulated.
Parameters___________________________________________
| list1 | On input, values to be sorted. On output, sorted values(i.e. list1[i] =< list1[i+1] ) |
| N | On input, length of lists to be sorted. |
| list2 | On input, a list associated with list1 . On output, if list1[k] on input is now stored in list1[j] on output, list2[k] on input is also stored as list2[j] on output. |
| list3 | On input, a list associated with list1 . On output, if list1[k] on input is now stored in list1[j] on output, list3[k] on input is also stored as list3[j] on output. Note: if list3 == NULL on input, it is unchanged on output. |
Aztec Functions
Prototype_____________________________________________
| void AZ_transform( | int *proc_config, int **external, int *bindx, double *val, int *update, int **update_index, int **extern_index, int **data_org, int N_update, int *indx, int *bpntr, int *rpntr, int **cpntr, int mat_type) |
Description_______________________________________
Convert the global matrix description to a distributed local matrix format
(see Section 2 and Section 6.4). See also AZ_reorder_vec and AZ_invorder_vec
to tranform the right hand side and solution vectors.
Parameters____________________________________________
| external | On output, allocated and set to components that must be communicated during the matrix vector multiply. |
| bindx, val, index, bpntr, rpntr | On input, matrix arrays (MSR or VBR) corresponding to global format. On output, matrix arrays (DMSR or DVBR) corresponding to local format. See Section 2. |
| update_index | On output, allocated and set such that update_index[i] is the local numbering corresponding to update[i]. |
| extern_index | On output, allocated and set such that extern_index[i] is the local numbering corresponding to external[i]. |
| data_org | On output, allocated and set to data layout informa tion, see Section 6.1. |
| cpntr | On output, allocated and set for VBR matrices to the column pointer array. |
| mat_type | On input, matrix format: either AZ_VBR_MATRIX or AZ_MSR_MATRIX. |
stAztec Functions
REFERENCES
| [1] S. | Carney, M. Heroux, and G. Li. A proposal for a sparse BLAS toolkit. Technical report, Cray Research Inc., Eagen, MN, 1993. | |
| [2] B. | Hendrickson and R. Leland. The Chaco user's guide - version 1.0. Technical Report Sand93-2339, Sandia National Laboratories, Albuquerque NM, 87185, August 1993. | |
| [3] J. | N. Shadid and R. S. Tuminaro. Sparse iterative algorithm software for large-scale MIMD machines: An initial discussion and implementation. Concurrency: Practice and Experience, 4(6):481-497, September 1992. | |
| [4] J. | N. Shadid and R. S. Tuminaro. Aztec - a parallel preconditioned Krylov solver library: Algorithm description version 1.0. Technical Report Sand95:in preparation, Sandia National Laboratories, Albuquerque NM, 87185, August 1995. | |
| [5] R. | S. Tuminaro, J. N. Shadid, and S. A. Hutchinson. Parallel sparse matrix vector multiply software for matrices with data locality. Submitted to BIT, August 1995. | |
| [6] Z. | Zlatev, V.A. Barker, and P.G. Thomsen. SSLEST - a FORTRAN IV subroutine for solving sparse systems of linear equations (user's guide). Technical report, Institute for Numerical Analysis, Technical University of Denmark, Lyngby,Denmark, 1978. |